Düzgün Dairesel Harekette İvme Nedir? Nasıl Hesaplanır? Örnekler

Düzgün dairesel harekette ivme nedir? Düzgün doğrusal harekette ivme nasıl hesaplanır, formülleri ve örneklerle anlatımı.

Kaynak: pixabay.com

Düzgün Dairesel Harekette İvme

Hızın değeri değişmeyip yönü değişse bile ivme vardır. Düzgün dairesel harekette de durum budur : Cisim çember üzerinde dolandıkça, hızın değeri değişmez ama yönü sürekli değişir. Bu nedenle de dairesel hareket ivmeli bir harekettir.

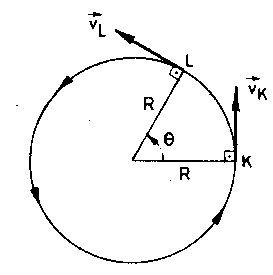
dairesel-harekette-ivme-1

Peki ivmenin değer ve yönü nedir, nasıldır? Şimdi bunu saptamaya çalışalım. Çember üzerinde değeri sabit hızla dolanan bir cisim, Şekildeki gibi, K noktasından geçerken hızı v_K, L noktasından geçerken v_L olsun. Bu iki vektörün değeri eşittir.

$\displaystyle {{\overrightarrow{a}}_{ort}}=\frac{\Delta v}{\Delta t}=\frac{\overrightarrow{{{v}_{son}}}-\overrightarrow{{{v}_{ilk}}}}{t}$

tanım bağıntısına göre ivmeyi saptamaya çalışalım. Bunun için de aşağıdaki şekildeki gibi, v_L vektörünü K noktasına taşıyarak Δv yi oluşturalım. Bilindiği üzere Δv, v_K nın ucundan v_L ye giden vektördür.

dairesel-harekette-ivme-2

$\displaystyle \left| \overrightarrow{{{v}_{K}}} \right|=\left| \overrightarrow{{{v}_{L}}} \right|$

olduğundan Şekilde v_K, v_L ve Δv vektörlerinin oluşturduğu üçgen, tepe açısı θ olan bir ikizkenar üçgendir. Bu üçgenin tabanı olan Δv ivmenin yönünü verir. Görülüyor ki ortalama ivmenin yönü çemberin dışından içine doğrudur.

Eğer cisim tam K noktasından geçerken ivmenin yönünü bulabilirsek, dairesel hareketin ivmesinin yönü bulunmuş olur. Bunun için de L noktasını K noktasına son derece yakın aldığımızı düşünelim. Bu durumda θ açısı sıfıra çok yakın olur. θ açısı sıfıra çok yakın olunca da, şekildeki ikizkenar üçgenin taban açıları 90° ye çok yakın olur. Bu da Δv nin v_K ya dikleşmesi demektir. Tam K noktasından geçerken ise Δv, v_K ya tam dik olur. Bundan da Δv nin merkeze yönelik olacağı çıkar.

O halde cisim K noktasından geçerken ivmenin yönü merkeze doğrudur. Bu düşünce çemberin tüm noktalarına uygulanırsa, ivme daima merkeze yönelik çıkar. Öyleyse düzgün dairesel harekette ivme, merkeze yöneliktir. Bu ivmeye merkezcil ivme denir.

Şimdi de ivmenin değerini bulalım :

Aşağıdaki şekildeki gibi v_K vektörünü L noktasına taşıyıp v_K, v_L, v vektörlerinin oluşturduğu üçgenle, R₁, R₂, üzerine kurulan üçgeni gözönüne alalım. Şekilde taralı olarak gösterilen bu iki üçgen benzerdir. Benzerlik bağıntısından,

dairesel-harekette-ivme-3

$\displaystyle \frac{\Delta v}{\left| KL \right|}=\frac{{{v}_{K}}}{{{R}_{1}}}=\frac{{{v}_{L}}}{{{R}_{2}}}$ olur. $\displaystyle {{v}_{K}}={{v}_{L}}={{v}_{1}}.{{R}_{1}}={{R}_{2}}=R$ olduğundan, $\displaystyle \frac{\Delta v}{\left| KL \right|}=\frac{v}{R}\Rightarrow \Delta v=\frac{v}{R}.\left| KL \right|$

elde edilir. Bu son eşitliğin iki yanını Δt ile bölersek $\displaystyle \frac{\Delta v}{\Delta t}=\frac{v}{R}.\frac{\left| KL \right|}{\Delta t}$ olur. Burada Δv/ Δt oranı ortalama ivmeyi, |KL| / Δt ortalama hızı vereceğinden,

$\displaystyle {{a}_{ort}}=\frac{v}{R}.{{v}_{ort}}$ elde edilir. L noktasını K noktasına son derece yaklaştırırsak a_ort = a. v_ort = v olur. Böylece, $\displaystyle a=\frac{v}{R}.v=\frac{{{v}^{2}}}{R}$ sonucuna varılır. Demek ki merkezcil ivme, çizgisel hızın karesiyle doğru orantılı, yarıçapla ters orantılıdır.