Düzgün Hızlanan Doğrusal Hareket Denklemleri (İvme Hız Konum)

Düzgün hızlanan doğrusal hareket nedir, düzgün hızlanan doğrusal hareket ivme, hız ve konum denklemleri nelerdir? Düzgün hızlanan doğrusal hareket bağıntıları.

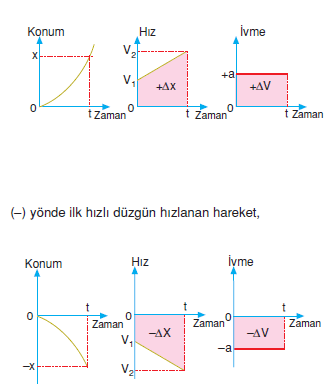
Düzgün Hızlanan Doğrusal Hareket

Bir doğru üzerinde hızlanarak yerdeğiştiren cismin çeşitli anlardaki hızının değerleri aşağıdaki çizelgede verilmiştir.

Zaman (s)	0	2	4	6	8
Hız (m/s)	6	9	12	15	18

Çizelgeden anlaşılacağı gibi, hız,her 2 saniyede bir 3 m/s artmaktadır. Yani ivme 1,5 m/s² dir ve sabittir. İşte böyle bir harekete düzgün hızlanan doğrusal hareket denir. O halde tanımı şöyle yapabiliriz :

Bir doğru üzerinde yerdeğiştiren cismin hızı, eşit zaman aralıklarında eşit artışlar gösteriyorsa bu harekete düzgün hızlanan doğrusal hareket denir.

Düzgün Hızlanan Doğrusal Hareket Denklemleri

1. İvme denklemi :

Hareketin tanımından da anlaşılacağı gibi ivme sabit ve pozitiftir. Pozitif ivme, hem hızın arttığını anlatır, hem de yönünün hareketle aynı olduğunu gösterir. O halde ivme denklemi,

$\displaystyle \overset{\to }{\mathop{a}}\,$ = Sabit (pozitif)

şeklindedir. Sabit ivmeli doğrusal hareketlerde ard arda gelen anlardaki hız değerleri, yukarıdaki çizelgede de görüldüğü gibi, bir aritmetik dizi oluştururlar. Böyle bir dizinin ortalama değeri, baştaki ve sondaki terimlerin toplamının yarısına eşittir. Bu nedenle düzgün hızlanan doğrusal harekette ortalama hız, ilk ve son hızların aritmetik ortalamasıdır.

$\displaystyle {{v}_{ort}}=\frac{{{v}_{ilk}}+{{v}_{son}}}{2}$

2. Hız denklemi :

Düzgün hızlanan doğrusal hareketin hız denklemini ivmenin tanım bağıntısından giderek çıkarabiliriz. İvmenin tanım bağıntısı,
$\displaystyle \overset{\to }{\mathop{a}}\,=\frac{\Delta \overset{\to }{\mathop{v}}\,}{\Delta \overset{\to }{\mathop{t}}\,}=\frac{\overset{{}}{\mathop{{{\overset{\to }{\mathop{v}}\,}_{son}}-\overset{{}}{\mathop{{{\overset{\to }{\mathop{v}}\,}_{ilk}}}}\,}}\,}{{{t}_{2}}-{{t}_{1}}}$

de vektörler yerine değerlerini koyabiliriz. Çünkü hareket doğrusaldır. Ayrıca t₂ = t, t₁ =0 alırsak,

$\displaystyle a=\frac{{{v}_{son}}-{{v}_{ilk}}}{t}$ den

$\displaystyle {{v}_{son}}={{v}_{ilk}}+at$

olur. Bu bağıntı, ilk hızı ve ivmesi bilinen bir hareketlinin t saniye sonundaki hızını hesaplamaya yarar ve hız denklemi adını alır.

3. Konum denklemi

Doğru boyunca yerdeğiştiren ve ivmesi a olan bir hareketli, t saniye sonunda x konumunda bulunuyor olsun.

$\displaystyle a=\frac{{{v}_{son}}-{{v}_{ilk}}}{t}$

$\displaystyle {{v}_{ort}}=\frac{{{v}_{ilk}}+{{v}_{son}}}{2}$

$\displaystyle {{v}_{ort}}=\frac{x}{t}$

bağıntıları arasında işlem yaparak x’i çözelim : İlk bağıntıdan bulunan

$\displaystyle {{v}_{son}}={{v}_{ilk}}+a.t$

değeri ikinci bağıntıda yerine yazılırsa

$\displaystyle {{v}_{ort}}=\frac{{{v}_{ilk}}+{{v}_{ilk}}+at}{2}={{v}_{ilk}}+\frac{1}{2}at$

elde edilir. Burada da V_ort yerine x/t yazılırsa

$\displaystyle \frac{x}{t}={{v}_{ilk}}+\frac{1}{2}at$

$\displaystyle x={{v}_{ilk}}t+\frac{1}{2}a{{t}^{2}}$

bulunur. Bu son bağıntı, ilk hızı ve ivmesi belli bir doğrusal harekette t saniye sonraki konumu bulmaya yarar. Ancak çok zorunlu olmadıkça bu bağıntıyı da kullanmayacağız. Özel olarak cisim dururken ivmelenmeye başlamışsa v_ilk = 0 olur ve konum denklemi, *

$\displaystyle x=\frac{1}{2}a{{t}^{2}}$