Son Yazılar :
NKFUCOM
NKFUCOM

Düzlemin Kapalı Denklemi

0
By on Bilgi Dünyası
Advertisement

12. sınıf geometri konusu, düzlemin kapalı denklemi Denklemi nedir, nasıl hesaplanır, örnek sorular.

Düzlemin Kapalı Denklemi


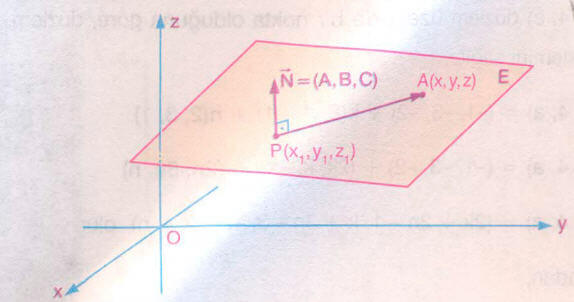
Yukarıdaki şekilde, \displaystyle P({{x}_{1}},{{y}_{1}},{{z}_{1}}) noktasından geçen ve normal vektörü \displaystyle \overrightarrow{N}=(A,B,C) olan E düzlemi veriliyor.,,

\displaystyle \overrightarrow{N} düzleme dik olduğundan, düzleme paralel veya düzlem üzerinde bulunan vektörlere de diktir.

Buna göre,

A(x, y, z), düzlem üzerinde herhangi bir nokta olmak üzere,

\displaystyle \overrightarrow{PA}\bot \overrightarrow{N} olur.

Advertisement

Dik iki vektörün Öklid iç çarpımı sıfıra eşit olduğundan,

\displaystyle \left\langle \overrightarrow{PA},\overrightarrow{N} \right\rangle =0 olur.

\displaystyle A\left( x-{{x}_{1}} \right)+B\left( y-{{y}_{1}} \right)+C\left( z-{{z}_{1}} \right)=0

eşitliğine düzlemin kapalı denklemi denir.

Örnek:

Uzayda, P(5, -1, 3) noktasından geçen ve \displaystyle \overrightarrow{N}=\left( 2,-4,5 \right) vektörüne dik olan düzlemin kapalı denklemini bulalım.

Advertisement

Çözüm:

A(x, y, z) düzlem üzerinde bir nokta olmak üzere,
\displaystyle \overrightarrow{PA}=A-P=\left( x-5,y+1,z-3 \right) olur.

Buna göre, düzlemin kapalı denklemi,

\displaystyle \left\langle \overrightarrow{PA},\overrightarrow{N} \right\rangle =0
2(x – 5) – 4(y + 1) + 5(z-3) = 0

2x- 10-4y-4 + 5z – 15 = 0

2x – 4y + 5z – 29 = 0 bulunur.

Örnek:

XYZ dik koordinat sisteminde, XOY, YOZ ve XOZ düzlemlerinin denklemlerini bulalım.

Çözüm:

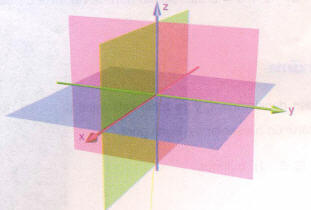
Koordinatları düzlemleri O(0, 0, 0) noktasında kesişmektedir. XOY düzleminin normal vektörü N1 = (0, 0, 1) dir.

Advertisement

XOY üzerindeki bir A(x, y, z) noktası için

\displaystyle \left\langle \overrightarrow{OA},\overrightarrow{{{N}_{1}}} \right\rangle =0

0 . x + 0 . y + 1 . z = 0 olduğundan, düzlem denklemi z = 0 bulunur.

Benzer şekilde,

YOZ düzleminin denklemi x = 0 ve
XOZ düzleminin denklemi y = 0 bulunur.

Tanım

A, B, C, D ∈ R için,

Ax + By + Cz + D = 0 eşitliğine düzlemin kapalı denklemi denir.

Bu eşitlikte x, y ve z nin katsayıları düzlemin normal vektörünün bileşenleridir.

\displaystyle \overrightarrow{N}=\left( A,B,C \right)

Bir P noktasından geçen ve N vektörüne dik olan düzlemin kapalı denkleminde,

Advertisement

\displaystyle D=-\left\langle \overrightarrow{OP},\overrightarrow{N} \right\rangle ile bulunur.

Örnek:

2x + 5y-z + 5 = 0 düzleminin normal vektörünü bulalım.

Çözüm

Verilen denklemde x, y ve z nin katsayıları düzlemin normal vektörünün bileşenleridir. Buna göre,

\displaystyle \overrightarrow{N}=\left( 2,5,-1 \right) bulunur.

ÖrneK

P(k, 1, -2) noktası 5x-3y + z- 5 = 0 düzlemi üzerinde olduğuna göre, k nın değerini bulalım.

Çözüm

P noktasının koordinatları düzlem denklemini sağlar. Buna göre, 5k-3-2-5 = 0

5k = 10 ⇒ k = 2 bulunur.

Advertisement

Örnek

F(2, 3, 4) noktası x + 2y-3z + D = 0 düzlemi üzerinde olduğuna göre, D nin değerini bulalım.

Çözüm

F noktasının koordinatları düzlem denklemini sağlar. Buna göre,

2 + 2- 3- 3- 4 + D = 0

2 + 6-12 + D = 0

-4 + D = 0 ⇒ D = 4 bulunur.


Leave A Reply