Son Yazılar :
NKFUCOM
NKFUCOM

Karmaşık Sayının Döndürülmesi

0
By on Bilgi Dünyası
Advertisement

Karmaşık sayıların döndürülmesi nasıl hesaplanır, örnek çözümlü sorular, karmaşık sayının döndürülmesi konu anlatımı.

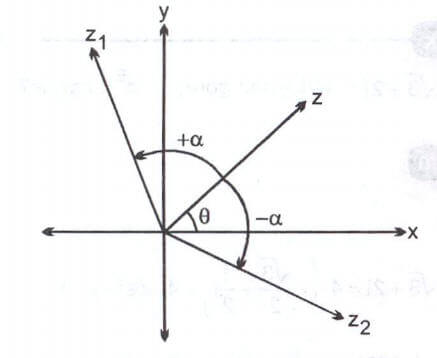
\displaystyle z=r.(\cos \theta +i.\sin \theta ) sayısı orijin etrafında, orijine olan uzaklığı değişmeksizin pozitif yönde \displaystyle \alpha açısı kadar döndürüldüğünde

\displaystyle {{z}_{1}}=r.\left[ \cos \left( \theta +\alpha \right)+i.\sin \left( \theta +\alpha \right) \right]=z.cis\alpha sayısı elde edilir.

Orijin etrafında, orijine olan uzaklığı değişmeksizin negatif yönde \displaystyle \alpha açısı kadar döndürüldüğünde

\displaystyle {{z}_{2}}=r.\left[ \cos \left( \theta -\alpha \right)+i.\sin \left( \theta -\alpha \right) \right]=z.cis\left( -\alpha \right) sayısı elde edilir.

karmasik-sayilarin-dondurulmesi

Advertisement

Örnek:

\displaystyle z=2cis35{}^\circ sayısının orijin etrafında pozitif yönde 10° döndürülmesiyle oluşan karmaşık sayıyı bulunuz.

Çözüm:

\displaystyle {{z}_{1}}=2cis35{}^\circ .cis10{}^\circ

\displaystyle {{z}_{1}}=2cis\left( 35{}^\circ +10{}^\circ \right)=2cis\left( 45{}^\circ \right)

\displaystyle =2\left( \cos 45{}^\circ +i.\sin 45{}^\circ \right)

Advertisement

\displaystyle =2\left( \frac{\sqrt{2}}{2}+i\frac{\sqrt{2}}{2} \right)=\sqrt{2}+i\sqrt{2}

Örnek:

\displaystyle z=\sqrt{3}-i sayısının orijin etrafında pozitif yönde 30° döndürülmesiyle oluşan karmaşık sayıyı bulunuz.

Çözüm:

\displaystyle z=\sqrt{3}-i (4. bölge)

\displaystyle \tan \theta =-\frac{1}{\sqrt{3}}\Rightarrow \theta =330{}^\circ

\displaystyle \left| z \right|=\sqrt{{{\left( \sqrt{3} \right)}^{2}}+{{\left( 1 \right)}^{2}}}=2

\displaystyle z=2.cis330{}^\circ

\displaystyle {{z}_{1}}=2.cis\left( 330{}^\circ +30{}^\circ \right)

\displaystyle =2.cis360{}^\circ =2\left( \cos 360{}^\circ +i.\sin 360{}^\circ \right)=2

Örnek:

Advertisement

z = 1 + 2i sayısı pozitif yönde 30° döndürülüyor. Elde edilen karmaşık sayıyı bulunuz.

Çözüm:

\displaystyle {{z}_{1}}=\left( 1+2i \right).cis30{}^\circ =\left( 1+2i \right).\left( \frac{\sqrt{3}}{2}+i\frac{1}{2} \right)

\displaystyle =\frac{\sqrt{3}}{2}+i\frac{1}{2}+i\sqrt{3}-1=\frac{\sqrt{3}-2}{2}+i\left( \frac{1+2\sqrt{3}}{2} \right)

Örnek:

z = 1 + i sayısı negatif yönde 45° döndürülüyor. Elde edilen karmaşık sayıyı bulunuz.

Çözüm:

\displaystyle {{z}_{1}}=\left( 1+i \right).cis\left( -45 \right){}^\circ =\left( 1+i \right).\left( \frac{\sqrt{2}}{2}-i\frac{\sqrt{2}}{2} \right)

\displaystyle =\frac{\sqrt{2}}{2}\left( 1+i \right)\left( 1-i \right)=\sqrt{2}


Leave A Reply