Son Yazılar :
NKFUCOM
NKFUCOM

Kuvvet Konu Anlatımı 10. Sınıf

0
By on Bilgi Dünyası
Advertisement

10. Sınıf fizik kuvvet konusu anlatımı. Kuvvetin özellikleri, bileşke kuvvetler, kesişen kuvvetlerin dengesi konu anlatımı, örnekler.

KUVVET

Cisimlerin şeklinde, hareket yönü ya da hızında değişikliğe neden olan etkiye kuvvet denir. Vektörel büyüklüktür ve dinamometre ile ölçülür.

Birimi Newtondur.

Bileşke kuvvet (R): iki veya daha fazla kuvvetin yaptığı etkiyi tek başına yapabilen kuvvete denir.

I. Kuvvetlerin Bileşkesi

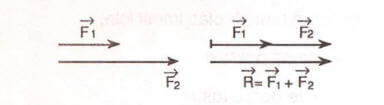
1.a Doğrultu ve yönleri aynı olan iki kuvvetin bileşkesi bu iki kuvvetin büyüklükleri toplamıdır. İki kuvvetin bileşkesinin maksimum değeridir.

Advertisement

kuvvet-1

1.b Doğrultuları aynı yönleri farklı iki kuvvetin bileşkesi büyüklüklerin farklarına eşit olup bileşkenin en küçük değeridir. F2 > F1 ise;

kuvvet-2

1.c İki kuvvet arasında herhangi bir a açısı varsa bileşkenin büyüklüğü kosinüs teoremi ile bulunur.

kuvvet-3

\displaystyle {{R}^{2}}=F_{1}^{2}+F_{2}^{2}+2{{F}_{1}}{{F}_{2}}\cos \alpha

Advertisement

ÖZEL DURUMLAR

***Eşit iki vektör arasındaki açı a ise bileşke vektör açıortay doğrultusundadır. Şiddeti ise, \displaystyle R=2F\cos \frac{\alpha }{2} bağıntısından hesaplanır.

***Eşit iki vektör arasındaki açı α ise, iki vektör farkı

\displaystyle R=2F\sin \frac{\alpha }{2} bağıntısından hesaplanır.

***İki kuvvet arasındaki açı α = 90° ise, pisagor bağıntısından, \displaystyle {{R}^{2}}=F_{1}^{2}+F_{2}^{2} olur.

***İki kuvvet arasındaki açı α = 90° ise ve kuvvetlerin büyüklükleri birbirine eşit ise, \displaystyle R=\sqrt{2}F

***İki eşit büyüklükteki kuvvet arasındaki açı α = 60° ise \displaystyle R=\sqrt{3}F

***İki eşit büyüklükteki kuvvet arasındaki açı α = 120° ise R=F

II. Paralel Kuvvetlerin Bileşkesi

II.a Aynı yönlü paralel kuvvetlerin bileşkesi

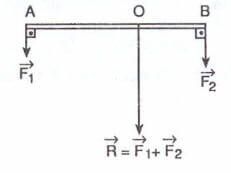
paralel-kuvvet

Advertisement

Aynı yönlü iki kuvvetin bileşkesi büyüklüklerinin toplamına eşit olup, bileşkenin uygulama noktası kuvvetler arasında ve büyük kuvvete yakındır. Bileşkenin uygulama noktasının yeri,
\displaystyle {{F}_{1}}\left| \overline{OA} \right|={{F}_{2}}\left| \overline{OB} \right| ile bulunur.

II.b Zıt yönlü paralel kuvvetlerin bileşkesi

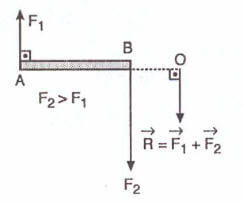
zit-kuvvet

Zıt yönlü paralel kuvvetlerin bileşkesi büyüklüklerinin farkına eşit olup uygulama noktası kuvvetlerin dışında, büyük kuvvet tarafında ve onun yönündedir. Bileşkenin uygulama noktasının yeri,

\displaystyle {{F}_{1}}\left| \overline{OA} \right|={{F}_{2}}\left| \overline{OB} \right| ile bulunur.

II.c Kuvvet çifti

Doğrultulan aynı şiddetleri eşit yönleri zıt iki kuvvet, kuvvet çifti oluşturur. Kuvvet çiftini oluşturan kuvvetlerin bileşkesi sıfır olmasına rağmen \displaystyle \left( \sum F=F-F=0 \right) cisim dönme hareketi yapar. Toplam moment sıfırdan farklıdır.

Kesişen Kuvvetlerin Dengesi

***Üç kuvvet dengede ise bunlar aynı düzlem içindedirler ve doğrultuları aynı noktadan geçer.

***Üç kuvvet dengede ise bunlardan birinin, diğer ikisi arasındaki açının sinüsüne oranı değişmez.
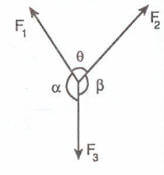
kesisen-kuvvet-1

\displaystyle \frac{{{F}_{1}}}{\sin \beta }=\frac{{{F}_{2}}}{\sin \alpha }=\frac{{{F}_{3}}}{\sin \theta }

Advertisement

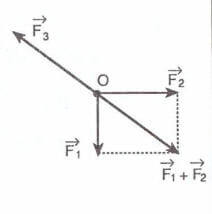
kesisen-kuvvet-2
***Kesişen üç kuvvet dengede ise, herhangi ikisinin bileşkesinin büyüklüğü üçüncü kuvvetle aynı büyüklükte ve zıt yöndedir.

\displaystyle \overrightarrow{{{F}_{3}}}=-\left( \overrightarrow{{{F}_{1}}}+{{\overrightarrow{F}}_{2}} \right)

\displaystyle \overrightarrow{{{F}_{1}}}+\overrightarrow{{{F}_{2}}}+\overrightarrow{{{F}_{3}}}=0


Leave A Reply