Sarkacın Periyotu Nasıl Hesaplanır? Formülü ve Deneysel Hesaplama

Bir sarkacın periyotu nasıl hesaplanır, nelere bağlıdır? Sarkaç formülü nedir? Sarkaç periyotunun deneysel ve formülle hesaplanması.

sarkaç

Sarkaç yaşamlarımızda oldukça yaygındır: eski zamanlardan kalma yavaşça salınan uzun bir sarkaçlı bir büyükbaba saati görmüş olabilirsiniz. Saati gösteren saat kadranındaki kadranları doğru şekilde ilerletmek için saatin çalışan bir sarkaça ihtiyacı vardır. Bu nedenle, saat üreticisinin bir sarkaç periyodunun nasıl hesaplanacağını anlaması gerekir.

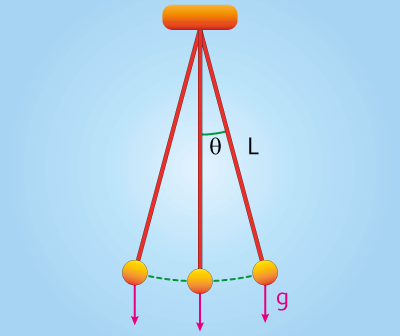
Sarkaç periyotu formülü T, oldukça basittir: $\displaystyle T={{\left( L/g \right)}^{1/2}}$ , burada g yerçekimi ivmesşidir ve L kütleye bağlı olan ipin uzunluğudur.

Bu miktarın boyutları saniye, saat veya gün gibi bir zaman birimidir.

Benzer şekilde, salınım frekansı f, 1 / T veya $\displaystyle f={{\left( g/L \right)}^{1/2}}$ ‘dir, bu da birim zaman başına kaç salınım olduğunu gösterir.

Kütle Farketmez

Bir sarkaç periyotu için bu formülün arkasındaki gerçekten ilginç olan kütlenin önemli olmadığıdır! Bu periyot formülü sarkaç hareket denkleminden türetildiğinde, kütlenin bağımlılığı iptal edilir. Öyle değilmiş gibi görünse de, kütlesinin bir sarkaç periyotunu etkilemediğini hatırlamak önemlidir.

… Ama bu Denklem Sadece Özel Koşullarda Çalışır

Bu formül olan $\displaystyle T={{\left( L/g \right)}^{1/2}}$ ‘nin sadece “küçük açılarda işe yaradığını hatırlamak önemlidir.

Peki küçük açı nedir ve neden böyle? Bunun nedeni, hareket denkleminin türetilmesinden kaynaklanmaktadır. Bu ilişkiyi türetmek için, işleve küçük açı yaklaşımını uygulamak gerekir: s sinüsü, burada θ, yörüngesindeki en düşük noktaya göre sarkaç açısıdır (genellikle ileri geri salındığı için izlediği yay.)

Küçük açı yaklaşımı yapılabilir çünkü küçük açılar için θ sinüsü neredeyse θ’ye eşittir. Salınım açısı çok büyükse, yaklaşım artık geçerli değildir ve bir sarkaç periyotu için farklı bir türev ve denklem gereklidir.

sarkaç periyotu

Bazı Basit Örnekler

Denklemin sadeliği ve denklemdeki iki değişkenin biri fiziksel bir sabit olduğu için, arka cebinizde tutabileceğiniz bazı kolay ilişkiler var!

Yerçekiminin ivmesi 9.8 m / s2’dir, bu nedenle bir metre uzunluğunda bir sarkaç için süre $\displaystyle T={{\left( 1/9,8 \right)}^{1/2}}=0,32$ saniyedir. Şimdi sarkacın 2 metre olduğunu söylesek? Yoksa 4 metre mi? Bu sayıyı hatırlamakla ilgili en uygun şey, bu sonucu, artışın sayısal faktörünün kare kökü ile ölçeklendirebilmenizdir, çünkü bir metre uzunluğunda bir sarkaç için süreyi bilirsiniz.

Bir Sarkaç Süresinin Ölçülmesi

Aşağıdakileri yaparak bir sarkaçın süresini kolayca ölçebilirsiniz.

Sarkacınızı istediğiniz gibi yapılandırın, ipin uzunluğunu bir desteğe bağlandığı noktadan sarkacın kütle merkezine kadar ölçün. Şimdi periyotu hesaplamak için formülü kullanabilirsiniz. Ama aynı zamanda sadece bir salınımı zamanlayabiliriz (veya birkaçını ölçebilir ve sonra ölçtüğünüz zamanı ölçtüğünüz salınım sayısına bölebiliriz) ve ölçümünüzü, formülün size verdiği sonuç ile karşılaştırabiliriz.

Basit Sarkaç Deneyi!

Denenmesi gereken bir diğer basit sarkaç deneyi, yer çekiminin yerel ivmesini ölçmek için bir sarkaç kullanmaktır.

Ortalama 9,8 m / s2 değerini kullanmak yerine, sarkacınızın uzunluğunu ölçün, periyodu ölçün ve yer çekimini hesaplamak için formülü kullanın. Aynı sarkacı bir tepenin üstünde ölçün.

Bir değişiklik fark ettiniz mi? Yerel yerçekimi ivmesinde bir değişiklik fark etmek için ne kadar yükseklik değişikliğine ulaşmanız gerekiyor?