Modüler Aritmetik Konu Anlatımı

Modüler aritmetik nedir, nasıl hesaplanır, özellikleri. Örneklerle modüler aritmetik konu anlatımı

MODÜLER ARİTMETİK

a, b sıfırdan farklı tamsayılar ve b>0 olmak üzere, a sayısını b ye bölmek demek, a = m.b+k, 0≤k

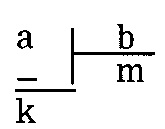
moduler-aritmetik-1

Bazı tam sayıların 3 ile bölme işlemini inceleyelim.

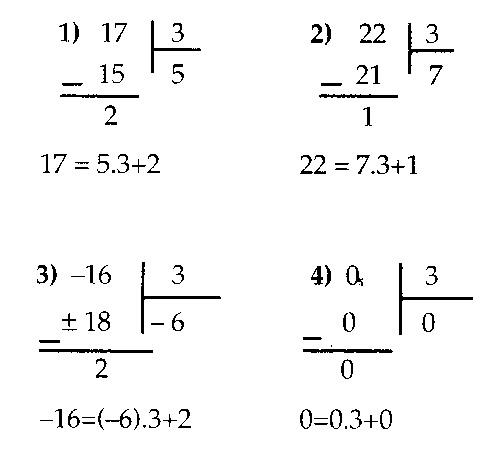
moduler-aritmetik-2

Sonuç: 3 ile bölümden kalanların 0,1,2 tamsayılardan biri olduğu görülüyor. Demek ki bir sayı 3 ile bölündüğünde 0,1,2 kalanlarını verir. Aşağıdaki kümeyi inceleyelim:

$\displaystyle \begin{array}{l}\overline{0}=\left\{ ....,-9,-6,-3,0,3,6,.... \right\}\\\overline{1}=\left\{ ....,-8,-5,-2,1,4,7,.... \right\}\\\overline{2}=\left\{ ....,-7,-4,-1,2,5,8,... \right\}\end{array}$

Burada; bir kümedeki her elemanın 3 ile bölümünden kalanın aynı olduğu, her kümedeki iki elemanın farkının 3 ile bölündüğünü ve bu kümelerin ayrık olup, birleşimlerinin de Zyi verdiğini görüyoruz.

Bu kümelerin z de

$\displaystyle \beta =\left\{ \left( x,y \right)\left| \left. 3 \right|x-y \right. \right\}$ bağıntısının denklik sınıfı oluşturduğunu biliyoruz.

$\displaystyle \left. 3 \right|\left( x-y \right)$ nin anlamı x-y = 3m (m∈Z) dir. Bu durum x = y (mod 3) yazılır ve “x’ denktir y modül 3” diye okunur.

$\displaystyle \begin{array}{l}x=3m+k,0\le k<3(k:Kalan)\\x-k=3m\Leftrightarrow x\equiv k(\bmod 3)\end{array}$

biçiminde yazılır. Bu ifade x ile k nın aynı denklik sınıfında olduğunu gösterir. Bu denklik sınıfı $\displaystyle k$ ile gösterilir ve

$\displaystyle \overline{k}=\left\{ x:x=3m+k;m,k\in z,0\le k<3 \right\}$

Tanım: a ve k tam sayıları ve m> o tamsayısı verilsin.

a-k farkı m ile tam bölünüyorsa, m modülüne göre a, k ya denktir denir ve a ≡ k (mod m) yazılır.

Yani, $\displaystyle \frac{a-k}{m}=b\in z\Leftrightarrow a\equiv k(\bmod m)$

Örnek: 3 Ι11-2 olduğundan
11 ≡ 2 (mod 3)
5 Ι12-(-3) olduğundan 12 ≡ -3 (mod 5)
5 Ι(-17)-(13) olduğundan
-17 ≡ 13 (mod 5)
3 modülüne göre kalan sınıfların kümesi Z/3,4 modülüne göre
Z/4, ……..m modülüne göre Z/m biçiminde gösterilir. bunlar,

$\displaystyle \begin{array}{l}Z/3=\left\{ \overline{0},\overline{1},\overline{2} \right\}\\Z/4=\left\{ \overline{0},\overline{1},\overline{2},\overline{3} \right\}\\--------------------\\Z/m=\left\{ \overline{0},\overline{1},\overline{2},.....\left( \overline{m-1} \right) \right\}\end{array}$