Atwood Makinesi Soruları Çözerken İzlenecek Yol, Problem Çözümü

Atwood Makinesi ile ilgili soruları çözerken izlenecek yol nasıl olmalıdır? Örnek soru ve çözümü ile atwood makinesi soruları ve formülleri.

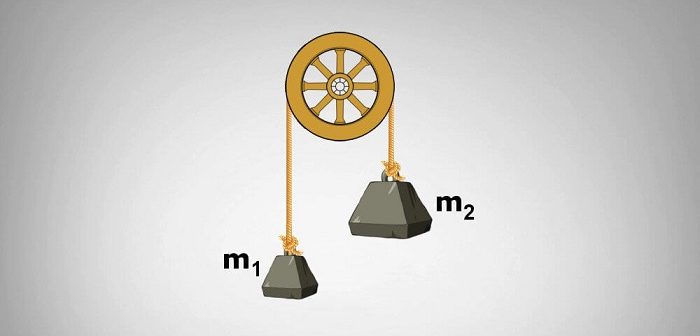
atwood makinesi

Atwood makine problemleri, bir kasnağın karşı taraflarına asılmış bir ip ile bağlanan iki ağırlık içerir. Bir Atwood Makinesi, kütlesiz bir kasnak üzerinde esnemeyen kütlesiz bir ip ile birleştirilmiş iki mA ve mB kütlesinden oluşur. İki kütle eşit olduğunda, sistem dengededir ve hareket olmaz. İki kütle sabit kalacaktır. İki ağırlık eşit olmadığında ise, sistem daha hafif kütle yukarı çekilirken daha ağır kütlenin aşağı çekildiği şekilde hareket edecektir. İpteki sistem ve ipteki gerilimin hesaplanması istenecektir. Aşağıdaki örnek problem, sistemin ivmesinin ve ipteki gerilimin nasıl hesaplanacağını gösterir.

Soru:

a) mA = 3 kg ve mB = 5 kg ise bir Atwood Makinesinin ivmesini bulun.
b) İki kütleyi birleştiren ipteki gerilimi bulun.

İşte makinanın bir örneği.

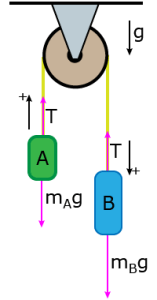
Atwood makinesi

Bu noktada cevabın nasıl bulunacağını göstermek için mA ve mB değerlerini göz ardı edeceğiz. B Blok, A Bloktan daha ağırdır, bu nedenle genel hareket yönü kasnağın B Blok tarafından aşağı ve A Blok tarafından yukarı doğru olacaktır. Hızlanma daima pozitif olacak şekilde, koordinat sisteminizi seçin.

Bu sistem kütlesiz ip ile birleştirilir. Daha ağır olan B Blok ipte bir süre içinde Δd mesafe aşağı çeker. Aynı zamanda, A Blok Δd yukarı çıkar. Bu, her bloğun hızlarının aynı olduğu anlamına gelir.

vA = Δd⁄t = vB

Hız yönleri, her bir sistem için seçilen koordinat sistemi ile ayarlanabilir. Hızlar her zaman aynı olduğundan, hızlanmaları (ivmeleri) aynıdır.

a = aA = aB (ivme)

İp kütlesiz ve uzatılamaz olduğundan, gerilim, sistem genelinde aynıdır. A bloğunu yukarı çeken gerilim B bloğunu yukarı çeken gerilim ile aynıdır.

Bu, ivme ve gerginliğin her iki blok için aynı olduğu anlamına gelir. Şimdi her bloğa etkiyen kuvvetleri bulalım.
A Blok için, gerilme kuvveti T yukarı doğru hareket ederken mAg ağırlığı aşağı doğru çekiyor.

ΣF = T – mAg

Hareket halinde olduğundan, bu kuvvetler mAa’ya eşittir.

ΣF = mAa = T – mAg

B Blok için kuvvetler neredeyse aynıdır. Aradaki fark, ivmenin A Blokunun ters yönünde olmasıdır.

ΣF = mBg – T = mBa

Şimdi iki denklemimiz ve iki bilinmeyenimiz var, T ve a. Bu iki denklemi bir araya getirdiğinizde T sadece ivme kalacak şekilde götürülür.

mAa = T – mAg
mBa = -T + mBg
mAa + mBa = mBg – mAg

Her iki taraftaki ivme ve yerçekimi değişkenlerini hesaba katın.

(mA + mB) a = (mB – mA) g
A’yı bulmak için her iki tarafı (mA + mB) ile bölün.
$\displaystyle a=\frac{\left( {{m}_{B}}-{{m}_{A}} \right)}{\left( {{m}_{A}}+{{m}_{B}} \right)}.g$

Şimdi ivmeyi bildiğimize göre, iki kuvvet denkleminden birini kullanarak gerilimi bulabiliriz. A Blokunu kullanalım.

mAa = T – mAg
T = mAa + mAg

A’nın değerini denkleme yerleştirin.

$\displaystyle T={{m}_{A}}\left( \frac{\left( {{m}_{B}}-{{m}_{A}} \right)g}{\left( {{m}_{A}}+{{m}_{B}} \right)} \right)+{{m}_{A}}g$
$\displaystyle T=\frac{\left( {{m}_{B}}-{{m}_{A}} \right){{m}_{A}}g}{\left( {{m}_{A}}+{{m}_{B}} \right)}+{{m}_{A}}g$
$\displaystyle T=\left( \frac{\left( {{m}_{B}}-{{m}_{A}} \right)}{\left( {{m}_{A}}+{{m}_{B}} \right)}+1 \right){{m}_{A}}g$
$\displaystyle T=\left( \frac{\left( {{m}_{B}}-{{m}_{A}} \right)}{\left( {{m}_{A}}+{{m}_{B}} \right)}+\frac{\left( {{m}_{A}}+{{m}_{B}} \right)}{\left( {{m}_{A}}+{{m}_{B}} \right)} \right){{m}_{A}}g$
$\displaystyle T=\left( \frac{{{m}_{B}}-{{m}_{A}}+{{m}_{A}}+{{m}_{B}}}{\left( {{m}_{A}}+{{m}_{B}} \right)} \right){{m}_{A}}g$
$\displaystyle T=\left( \frac{2{{m}_{B}}}{\left( {{m}_{A}}+{{m}_{B}} \right)} \right){{m}_{A}}g$
$\displaystyle T=\frac{2{{m}_{A}}{{m}_{B}}g}{\left( {{m}_{A}}+{{m}_{B}} \right)}$

Şimdi ivme ve gerilme için formüller ürettiğimize göre, ilk sorunun cevabını bulabiliriz.

***mA = 3 kg ve mB = 5 kg olduğunda ivmeyi bulalım.

$\displaystyle a=\frac{\left( {{m}_{B}}-{{m}_{A}} \right)}{\left( {{m}_{A}}+{{m}_{B}} \right)}g=\frac{\left( 5kg-3kg \right)}{\left( 5kg+3kg \right)}g=2/8g=0,25(9,8m/{{s}^{2}})=2,54m/{{s}^{2}}$

***İpteki gerilimi bulalım.

$\displaystyle T=\frac{2{{m}_{A}}{{m}_{B}}g}{\left( {{m}_{A}}+{{m}_{B}} \right)}=\frac{2(3kg)\left( 5kg \right)\left( 9,8m/{{s}^{2}} \right)}{\left( 3kg+5kg \right)}=\frac{294k{{g}^{2}}m/{{s}^{2}}}{8kg}=36,75kgm/{{s}^{2}}=36,75N$

İpucu: Bu tür sorunların anahtarı, ivme yönü daima pozitif yönde olacak şekilde koordinat sisteminizi seçmektir. Atwood makinesinde ivme daima daha büyük kütleye doğru ilerler.