Bir dairenin alanı nasıl hesaplanır? Dairenin alan formülü ve açıklaması, hesaplama örneği. Dairenin alanı hesaplaması konu anlatımı
Dairenin Alanı Nasıl Bulunur?
Bir daire, sabit bir noktadan eşit uzaklıkta olan bir dizi noktadan oluşan, sınırları olan yuvarlak bir düzlem şeklidir. Bu nokta dairenin merkezi olarak bilinir. Daireyle ilgili birçok ölçüm var. Bir çemberin çevresi esasen şeklin etrafındaki ölçümdür. Çevreleyen sınır veya kenardır. Bir dairenin yarıçapı, dairenin merkez noktasından dış kenarına doğru olan düz bir çizgi parçasıdır. Bu, dairenin merkez noktası ve bitiş noktası olarak dairenin kenarındaki herhangi bir nokta kullanılarak ölçülebilir. Bir dairenin çapı, dairenin bir kenarından diğerine, merkezden geçen düz çizgi ölçümüdür.
Bir dairenin yüzey alanı için formül ‘dir, burada A dairenin alanıdır ve r dairenin yarıçapıdır.
Bir dairenin yüzey alanı veya herhangi bir iki boyutlu kapalı eğri, bu eğrinin içerdiği toplam alandır. Bir dairenin alanı, yarıçapı, çapı veya çevresinin uzunluğu bilindiğinde hesaplanabilir.
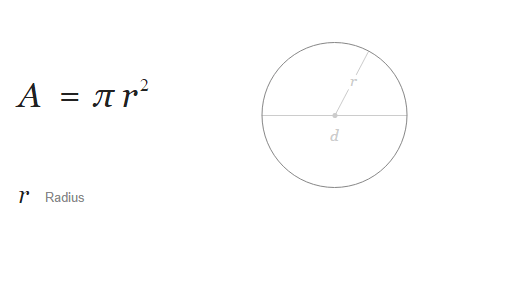
Pi’ye Giriş
Bir dairenin alanını hesaplamak için Pi kavramını anlamanız gerekir. Matematik problemlerinde π (Yunan alfabesinin on altıncı harfi) ile gösterilen Pi, bir dairenin çevresinin çapına oranı olarak tanımlanır. Çevrenin çapa sabit bir oranıdır. Bu, π = c / d anlamına gelir; c, bir dairenin çevresidir ve d, aynı dairenin çapıdır.
π’nin kesin değeri asla bilinemez, ancak istenen herhangi bir kesinliğe göre tahmin edilebilir. π ila altı ondalık basamağın değeri 3.141593’dür. Bununla birlikte, ondalık basamakları belirli bir desen veya son olmadan devam eder ve devam eder, bu nedenle çoğu uygulamada π değeri, özellikle kalem ve kağıt ile hesaplanırken, geleneksel olarak 3.14 olarak kısaltılır.
Bir Dairenin Alan Formülü
“Bir dairenin alanı” formülünü inceleyin: , burada A dairenin alanı ve r dairenin yarıçapıdır. Arşimed bunu M.Ö. 260 yılında kanıtlamıştır.
Alan Formülünü Uygulamak
Yarıçapı 2 olan bir dairenin alanını bulmanız istendiğini hayal edin.
Bu dairenin alanı için formül ‘dir.
Bilinen r değerini denklemin içine yerleştirmek size A = π (2²) = π (4) ‘i verir.
π için kabul edilen 3.14 değerini değiştirerek, A = 4 × 3.14 veya yaklaşık olarak 12,57 değerini buluruz.
Çapı Kullanarak Hesaplama
Dairenin çapını kullanarak alanı hesaplamak için dairenin alanı formülünü dönüştürebilirsiniz, 2 r = d olacaktır. Çap yarıçapın iki katıdır. Her bir tarafı 2’ye bölerseniz, sonuç r = d / 2 olur. Bunu bir dairenin alanı için genel formüle yerleştiririz: