Dik dairesel silindirin alanı nasıl hesaplanır? Dik dairesel silindirin alan formülü, örnek soru ve çözümlerle hesaplanması.
Dik Dairesel Silindirin Alanı
Dik dairesel silindirin açınımı, silindirin yanal yüzünü oluşturan bir dikdörtgen ve tabanlarını oluşturan iki daireden oluşur.
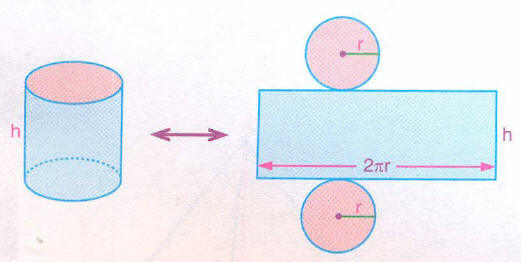
Silindirin Açılımı
Açınımda silindirin yanal yüzünü oluşturan dikdörtgenin bir kenarı silindirin yüksekliğine, diğer kenarı ise silindirin taban çevresine eşittir. Buna göre,
dik dairesel silindirin yanal alanı, taban çevresi ile yüksekliğinin çarpımına eşittir.
Ay = Taban çevresi * Yükseklik
Silindirin alanı, taban alanının iki katı ile yanal alanının toplamına eşittir.
Yüksekliği h, taban yarıçapı r olan silindirin alanı,
olur.
Örnek
Yüksekliği 8 cm, taban yarıçapı 6 cm olan bir dik silindirin alanını bulalım.
Çözüm
Silindirin taban alanı,
cm² dir.
Yanal alanı,
cm² dir.
Silindirin Alanı = Yanal Alanı + 2 * Taban Alanı
cm² bulunur.