Advertisement
İşaret fonksiyonu nedir? İşaret fonksiyonu özellikleri nelerdir? Hesaplanması, örnekleri, soruların çözümleri, konu anlatımı.

İşaret fonksiyonu, matematikte sık kullanılan bir fonksiyondur. Genellikle $sgn(x)$ veya $\mathrm{sign}(x)$ ile gösterilir ve bir gerçek sayıyı girdi olarak alır ve onun pozitif, negatif veya sıfır olduğunu belirten bir çıktı üretir. Yani işaret fonksiyonu, girdi sayısının işaretine (pozitif, negatif veya sıfır) bağlı olarak, sırasıyla -1, 0 veya 1 değerlerini verir. Bu fonksiyon, matematiksel işlemlerde, özellikle de fonksiyonların davranışlarını incelemek için kullanılır.
İŞARET FONKSİYONU KONU ANLATIMI
olmak üzere
fonksiyonu için
şeklinde tanımlanan fonksiyonunu f nin işaret fonksiyonu denir.
Advertisement
ÖRNEK:
denkleminin R deki çözüm kümesini bulalım.
olması gerekir.
olur.

ÖRNEK:
- fonksiyonunun en geniş tanım kümesini yazalım.
olması gerekir.
olur.

ÖRNEK:
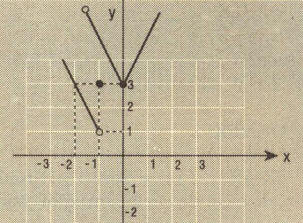
eşitsizliğinin R deki çözüm kümesini yazalım.
- Sgn f(x) in 1/3 ten büyük olduğu değerler için f(x)>0 olmalıdır.
Buna göre;
Ç= R-[-3/2,-1] olur.
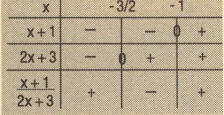
ÖRNEK:
fonksiyonu parçalı bir biçimde yazalım ve grafiğini çizelim.

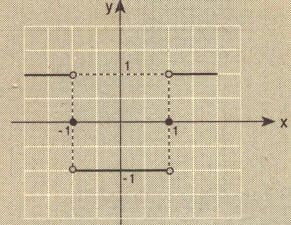
ÖRNEK:
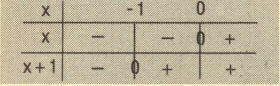
- (gof)(x) fonksiyonunu parçalı bir biçimde yazıp grafiğini çizelim.
Advertisement