Kütle çekim potansiyel enerjisi nedir? Kütle çekim potansiyel enerjisi nelere bağlıdır, formülü, hesaplanması, konu anlatımı.
Kütle Çekim Potansiyel Enerjisi
Kütlesi olan her varlık bir çekim kuvveti yaratır. Cisimler bir arada bulunurken birbirlerine uyguladıkları çekim kuvveti nedeniyle bir potansiyel enerjiye sahip olurlar. Bu potansiyel enerji ancak sonsuzda sıfırdır. Çünkü sonsuz uzaklıkta çekim kuvveti sıfır olur. Üstelik potansiyel enerji sonsuzda maksimum değere de sahiptir. Çünkü birbirini çeken iki cismi ne denli uzaklaştırırsak o kadar çok iş yaparız. Yapılan bu iş sistemin potansiyel enerjisini artırır. Demek ki birbirini çeken cisimleri uzaklaştırdıkça sisteme daha çok enerji depolanmaktadır. İşte bu nedenle kütleler sonsuz uzaklıktayken maksimum enerjiye sahiptirler. Buna göre ortaya şöyle bir durum çıkıyor : Potansiyel enerji sonsuzda hem sıfır hem de maksimum. Bu nasıl olur? Nasıl bir değişim bunu sağlar? Artarak sıfıra giden bir değişim bunu sağlar. Bu da başlangıcın negatif değerlerde olmasıyla mümkündür. Ancak negatif değerler alarak artan değişkenler bu değişime uyar. Öyleyse çekim potansiyel enerjisi negatif olmalıdır.
İki kütleyi birbirinden uzaklaştırırken çekim kuvvetine karşı bir iş yaparız. Yapılan bu iş kütleler sistemine potansiyel enerji olarak depolanır. O halde çekim kuvvetini yenmek için yapılan iş, potansiyel enerjideki artışa eşit olacaktır.
Formül:
- (Çekim kuvvetine karşı yapılan iş) = (Son potansiyel enerji) – (İlk potansiyel enerji)
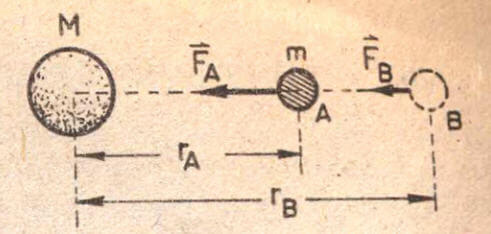
- Şekildeki m kütleli cismi A dan B ye sabit hızla götürdüğümüzü düşünelim : AB yolu boyunca yapılan iş,
- Kuvvet, uzaklığın karesiyle ters orantılı olarak değiştiğinden ortalama kuvvet, A ve B deki kuvvetlerin geometrik ortalamasıdır. Böylece,
- olur.
olduğundan,
- elde edilir. Burada A ve B ye ait terimler eşleştirilirse,
- olur. Görülüyor ki A ve B noktalarına ait potansiyel enerjileri veren bağıntılar negatiftir. O halde genel olarak çekim potansiyel enerjisi,
- dir. Burada M ve m=kilogram, r=metre,
alınarak PE =Joule çıkar.