Son Yazılar :
NKFUCOM
NKFUCOM

Mutlak Değer Fonksiyonu, Grafik ve Örnekler

0
By on Bilgi Dünyası
Advertisement

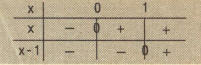
Mutlak değer fonksiyonu nedir, özellikleri nelerdir? Grafikler ve örneklerle açıklaması, çözümlü sorular.

Mutlak Değer Fonksiyonu

\displaystyle A\subset R olmak üzere \displaystyle f:A\to R fonksiyonu için

\displaystyle f(x)=\left| f(x) \right|=f(x);f(x)\ge 0

\displaystyle f(x)=\left| f(x) \right|=-f(x);f(x)<0

şeklinde tanımlanan \displaystyle \left| f \right|:A\to R fonksiyonuna f fonksiyonunun mutlak değer fonksiyonu denir.

Advertisement

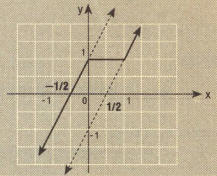
ÖRNEK: \displaystyle f:R\to R,f(x)=\left| x-1 \right| fonksiyonunun parçalı biçimde gösterelim ve grafiğini çizelim.

mutlak-deger-fonksiyon

\displaystyle f(x)=x-1;x\ge 1

\displaystyle f(x)=-\left( x-1 \right);x<1

Not: \displaystyle \left| f(x) \right| in grafiğini çizmek için önce f(x) in grafiği çizilir. x ekseninin altında kalan parçaların x eksenine göre simetriği alınır.

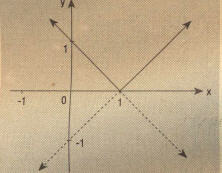
ÖRNEK: \displaystyle f:R\to R,f(x)=\left| 4-{{x}^{2}} \right| fonksiyonu parçalı biçimde yazalım ve grafiğini çizelim.

Advertisement

mutlak-deger-fonksiyon-1

\displaystyle 4-{{x}^{2}}=0\Rightarrow x=\pm 2

\displaystyle f(x)={{x}^{2}}-4;x< -2

\displaystyle f(x)=4-{{x}^{2}};-2\le x\le 2

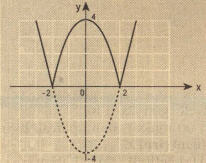
mutlak-deger-fonksiyon-2

ÖRNEK:

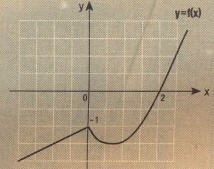
mutlak-deger-fonksiyon-3

\displaystyle f:R\to R fonksiyonunun grafiği veriliyor.

\displaystyle g(x)=\frac{f(x)-\left| f(x) \right|}{2} şeklinde tanımlı g(x) fonksiyonunu parçalı bir biçimde yazalım ve grafiğini çizelim.

\displaystyle f(x)\ge 0\Rightarrow g(x)=\frac{f(x)-f(x)}{2}\Rightarrow g(x)=0

\displaystyle f(x)<0\Rightarrow g(x)=\frac{f(x)+f(x)}{2}\Rightarrow g(x)=f

Advertisement

olur. Buna göre

\displaystyle g(x)=0;f(x)\ge 0

\displaystyle g(x)=f(x);f(x)<0

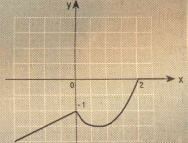
mutlak-deger-fonksiyon-4

ÖRNEK:

\displaystyle f(x)=2x-\sqrt{{{x}^{2}}}+\sqrt{{{x}^{2}}-2x+1} fonksiyonunu parçalı bir biçimde gösterelim ve grafiğini çizelim.

\displaystyle f(x)=2x-\sqrt{{{x}^{2}}}+\sqrt{{{x}^{2}}-2x+1}

\displaystyle f(x)=2x-\left| x \right|+\sqrt{{{\left( x-1 \right)}^{2}}}

\displaystyle f(x)=2x-\left| x \right|+\left| x-1 \right|

mutlak-deger-fonksiyon-5
\displaystyle f(x)=2x+x-x+1;x<0
\displaystyle f(x)=2x-x-x+1;0\le x<1
\displaystyle f(x)=2x-x+x-1;x\ge 1

\displaystyle f(x)=2x+1;x<0
\displaystyle f(x)=1;0\le x<1
\displaystyle f(x)=2x-1;x\ge 1
mutlak-deger-fonksiyon-6

Advertisement


Leave A Reply