Seva Teoremi ve İspatı

Seva teoremi nedir? Seva teoreminin formülü, açıklaması ve ispatı.

SEVA TEOREMİ

seva-teoremi

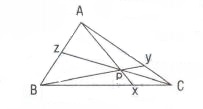
ABC üçgeninin iç bölgesindeki bir P noktasını köşelere birleştiren doğrular kenarları sırası ile x, y, z noktalarında keser ise :

$\displaystyle \frac{\left| XB \right|}{\left| XC \right|}.\frac{\left| YC \right|}{\left| YA \right|}.\frac{\left| ZA \right|}{\left| ZB \right|}=1$

İSPAT:

ABX üçgeninin kenarları z, p, c noktalarında kesilmiştir. Bu üçgene Menalaüs Teoremi uygulanır ise:

$\displaystyle \frac{\left| ZA \right|}{\left| ZB \right|}.\frac{\left| CB \right|}{\left| CX \right|}.\frac{\left| PX \right|}{\left| PA \right|}=1\to \left( 1 \right)$

AXC üçgenine Menalaüs teoremi uygulanır ise:

$\displaystyle \frac{\left| PA \right|}{\left| PX \right|}.\frac{\left| BX \right|}{\left| BC \right|}.\frac{\left| yC \right|}{\left| yA \right|}=1\to (2)$

bulunur.

(1) ve (2) eşitlikleri taraf tarafa çarpılır ise :

$\displaystyle \frac{\left| ZA \right|}{\left| ZB \right|}.\frac{\left| CB \right|}{\left| CX \right|}.\frac{\left| PX \right|}{\left| PA \right|}.\frac{\left| PA \right|}{\left| PX \right|}.\frac{\left| BX \right|}{\left| BC \right|}.\frac{\left| yC \right|}{\left| yA \right|}=1$

Gereken kısaltmalar yapılır ise:

$\displaystyle \frac{\left| ZA \right|}{\left| ZB \right|}.\frac{\left| XB \right|}{\left| XC \right|}.\frac{\left| yC \right|}{\left| yA \right|}=1$ bulunur.