Sinüs, kosinüs, tanjant, kotanjant nedir, değerleri nelerdir? Sinüs kosinüs nasıl hesaplanır, sinüs eğrisi nedir, hakkında bilgi.
SİNÜS, KOSİNÜS
Matematikte kullanılan bazı değerlerin genel adıdır. Matematikte ve matematiğin kullanıldığı bilim kollarında hesapların yapılmasını çok kolaylaştırır. Sinüs kadar kullanılan üç değer daha vardır. Bunlar, «kosinüs», «tangent», «kotangent»tir. Bu dört değerde bunlara benzer değerlerin hesaplanması, aralarındaki bağıntıların bulunmasıyla ilgilenen matematik koluna «trigonometri» denir.
Sinüs. — Bir dik üçgende, dar açının karşısındaki kenarın uzunluğunun, hipotenüsün (dik açının karşısındaki kenarın) uzunluğuna oranı bize, o açının sinüsünü verir. Bir dik üçgende hipotenüs her zaman en uzun kenar olduğu için bu oran hep l’den küçüktür. Buna göre, sinüs her zaman l’den küçük bir sayıdır. Örnek olarak, kenarları 3, 4, 5 cm. olan bir dik üçgen düşünelim. En uzun kenar olan hipotenüs 5 cm.’dir. Öyleyse, 3 cm.’lik kenarın karşısındaki açının sinüsünü hesaplamak için 3’ün 5’e oranını bulmamız gerekir.
Kosinüs. — Bir açının yanındaki kenarın, hipotenüse oranıdır. Yukarıdaki örnekte:
cos A = 4/5 = 0,8
Tangent. — Bir açının karşısındaki kenarın, komşu kenara oranı, bize o açının tangentini verir:
tg A= 3/4 = 0,75
Kotangent. — Tangentin tersine verilen addır. Buna göre, bir açının komşu kenarının uzunluğunun, karşı kenarın uzunluğuna oranı bize o açının kotangentini verir:
cotg A= 4/3 = 1,35
Trigonometride her açıya karşılık sinüs, kosinüs, tangent, kotangent değerleri hesaplanarak cetveller hazırlanmıştır. İşlemler sırasında kaç derecelik bir açıyla karşılaşılırsa, o cetvellere bakılarak, açının trigonometrik fonksiyonlarının değeri bulunur.
Trigonometride «sinüs teoremi», «kosinüs teoremi» adını alan iki teorem vardır. Bu teoremler trigonometrik işlemlerin yapılmasında ve trigonometrik denklemlerin çözülmesinde kolaylık sağlarlar.
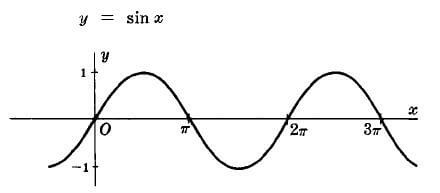
Sinüs Eğrisi
A açısını sıfırdan başlayarak büyüttüğümüzü düşünelim. Açı büyüye büyüye 180° olacaktır. A açısının her değerinde sinüsünü de hesaplayıp açıyı, açılara karşılık olan sinüs değerlerini bir cetvel halinde düzenleyelim. Sonra birbirine dik iki eksen, yani bir koordinat takımı alalım. Bu iki eksenden yatay olanı üzerinde açıları işaretleyelim. Düşey eksenin bölümleri ise bize sinüsleri göstersin. Hazırladığımız cetvelden açıları, açılar eksenine; sinüsleri de sinüsler eksenine taşıyalım. Bulduğumuz noktaları birleştirelim. Zikzaklı bir eğri elde ederiz. Bu eğriye «sinüsoit», ya da «sinüs eğrisi» denir.
Titreşim hareketi yapan cisimlerin hareketlerinin incelenmesi sırasında, alternatif elektrik akımının değişiminin araştırılamsında sinüsitle çok karşılaşılır. Şehir şebekelerinde kullandığımız elektrik akımı «sinüsoidal alternatif akım»dır.