Yatay Asimptot Nasıl Bulunur? Hesaplanması Örnek Soru Çözümleri

Yatay Asimptot nedir, nasıl bulunur? Yatay Asimptot hesaplanması, çözümleriyle soru örnekleri, üstel ve rasyonel fonksiyonlarda çözümler.

Yatay Asimptot Nedir?

Bir asimptot, belirli bir eğriye keyfi olarak yaklaşan bir çizgi veya eğridir. Başka bir deyişle, belirli bir eğriye yakın bir çizgidir, öyle ki eğri ile çizgi arasındaki mesafe, eğri daha yüksek / düşük değerlere ulaştığında sıfıra yaklaşır. Asimptotlu eğrinin bölgesi asimptotiktir. Asimptotlar genellikle rotasyonel fonksiyonlarda, üstel fonksiyonda ve logaritmik fonksiyonlarda bulunur. X eksenine paralel asimptot, yatay eksen olarak bilinir.

Yatay Asimptot Nasıl Bulunur?

Bir eğrinin işlevi aşağıdaki koşulu yerine getiriyorsa bir asimptot vardır. Eğer f (x) eğri ise, o zaman yatay bir asimptot mevcutsa,

$\displaystyle \underset{{x\to +\infty }}{\mathop{{\lim }}}\,f\left( x \right)=C$

veya

$\displaystyle \underset{{x\to -\infty }}{\mathop{{\lim }}}\,f\left( x \right)=C$

O zaman, y = C denklemi ile yatay asimptotlar mevcuttur. İşlev sonsuzda sonlu değere (C) yaklaşırsa, işlevin bu değerde bir asimptot vardır ve bir asimptotun denklemi y = C’dir. Bir eğri bu çizgiyi birkaç noktada kesebilir, ancak sonsuza yaklaştıkça asimtotik hale gelir.

Belirli bir fonksiyonun asimptotunu bulmak için, sonsuzda sınırları bulun.

Yatay asimptotları bulma – Örnekler

Üstel form fonksiyonları 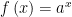$\displaystyle f\left( x \right)={{a}^{x}}$ ve [a>0]

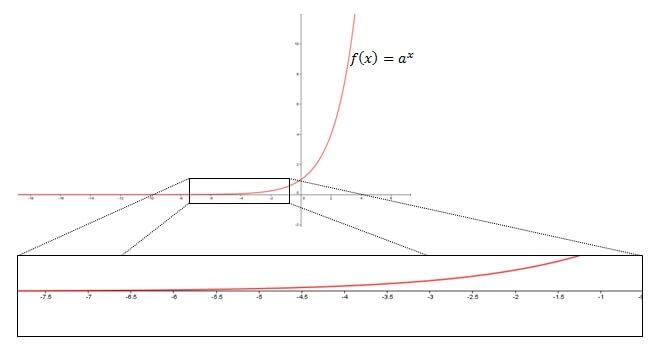
Yatay Asimptot

Üstel fonksiyonlar, yatay asimptotların en basit örnekleridir. Fonksiyonun limitlerini pozitif ve negatif sonsuzlarda almak, $\displaystyle \underset{{x\to \infty }}{\mathop{{\lim }}}\,{{a}^{x}}=+\infty$ ve $\displaystyle \underset{{x\to -\infty }}{\mathop{{\lim }}}\,{{a}^{x}}=0$ verir. Sağ sınır sonlu bir sayı değildir ve pozitif sonsuza meyillidir, ancak sol sınır 0 sonlu değerlerine yaklaşır.

Bu nedenle, $\displaystyle f\left( x \right)={{a}^{x}}$ üstel fonksiyonunun 0’da yatay bir asimptota sahip olduğunu söyleyebiliriz. Asimptot çizgisinin denklemi, aynı zamanda x ekseni olan y = 0’dır. A herhangi bir pozitif sayı olduğu için, bunu genel bir sonuç olarak kabul edebiliriz.

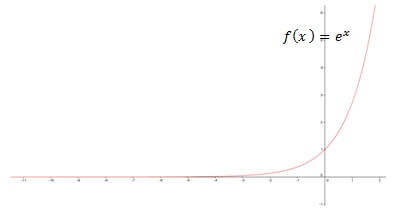
A = e = 2,718281828 olduğunda, fonksiyon üstel fonksiyon olarak da bilinir. $\displaystyle f\left( x \right)={{e}^{x}}$ belirli özelliklere sahiptir ve bu nedenle matematikte önemlidir.

Yatay Asimptot

Rasyonel fonksiyonlar

F (x) = h (x) / g (x) formundaki bir fonksiyon, burada h (x), g (x) polinomlardır ve g (x) ≠ 0, rasyonel fonksiyon olarak bilinir. Rasyonel işlev hem dikey hem de yatay asimptotlara sahip olabilir.

i. F (x) = 1 / x fonksiyonunu düşünün

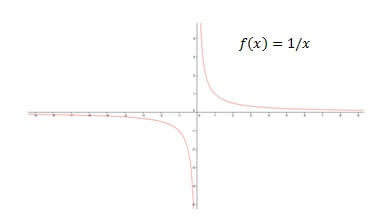
Yatay Asimptot

F (x) = 1 / x fonksiyonunun hem dikey hem de yatay asimptotları vardır. Yatay asimptot bulmak için sonsuzda sınırları bulun.

$\displaystyle \underset{{x\to }}{\mathop{{\lim }}}\,=+\infty$ $\displaystyle 1/x={{0}^{+}}$ ve $\displaystyle \underset{{x\to }}{\mathop{{\lim }}}\,=-\infty$ $\displaystyle 1/x={{0}^{-}}$

X → + ∞, fonksiyon pozitif taraftan 0’a, x → = -∞ fonksiyonu negatif yönden 0’a yaklaştığında;

Fonksiyon sonsuzluklara yaklaşırken 0 sonlu değerine sahip olduğundan, asimptotun y = 0 olduğu sonucuna varabiliriz.

ii. F (x) = 4x / (x2 + 1) fonksiyonunu düşünün

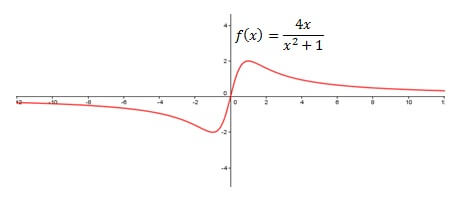
Yatay Asimptot

Yatay asimptoti belirlemek için yine sonsuzda sınırları bulun.

$\displaystyle \underset{{x\to +\infty }}{\mathop{{\lim }}}\,=\frac{{4x}}{{{{x}^{2}}+1}}=\underset{{x\to +\infty }}{\mathop{{\lim }}}\,\frac{4}{{x+\frac{1}{x}}}=0$

$\displaystyle \underset{{x\to -\infty }}{\mathop{{\lim }}}\,=\frac{{4x}}{{{{x}^{2}}+1}}=\underset{{x\to -\infty }}{\mathop{{\lim }}}\,\frac{4}{{x+\frac{1}{x}}}=0$

Yine fonksiyon asimptot y = 0’a sahiptir, bu durumda da fonksiyon asimptot çizgisiyle x = 0’da kesişir.

iii. 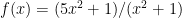$\displaystyle f(x)=(5{{x}^{2}}+1)/({{x}^{2}}+1)$ fonksiyonunu düşünün

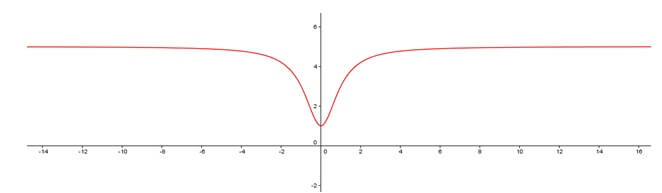
Yatay Asimptot

Sınırları sonsuzda alırsak,

$\displaystyle \underset{{x\to +\infty }}{\mathop{{\lim }}}\,\frac{{5{{x}^{2}}+1}}{{{{x}^{2}}+1}}=\underset{{x\to +\infty }}{\mathop{{\lim }}}\,\frac{{5+\frac{1}{{{{x}^{2}}}}}}{{1+\frac{1}{{{{x}^{2}}}}}}=5$

$\displaystyle \underset{{x\to -\infty }}{\mathop{{\lim }}}\,\frac{{5{{x}^{2}}+1}}{{{{x}^{2}}+1}}=\underset{{x\to -\infty }}{\mathop{{\lim }}}\,\frac{{5+\frac{1}{{{{x}^{2}}}}}}{{1+\frac{1}{{{{x}^{2}}}}}}=5$