Düzgün dörtyüzlünün özellikleri, alanı ve hacmi nasıl hesaplanır? Düzgün dörtyüzlünün alan, hacim formülleri, örnek sorular ve çözümleri.
Düzgün Dörtyüzlü Nedir?
Dört yüzü birbirine eş ve eşkenar üçgen olan piramide düzgün dörtyüzlü denir.
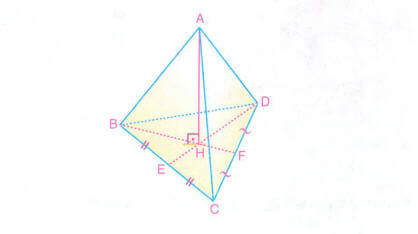
Piramidin yükseklik ayağı tabandaki eşkenar üçgenin ağırlık merkezidir.
Örnek
Şekilde, bir köşesi orijinde olan düzgün dörtyüzlünün bir köşesi B(0, 6, 0) dır.
Buna göre, düzgün dörtyüzlünün dikme ayağının ve köşelerinin koordinatlarını bulalım.
Çözüm
Düzgün dörtyüzlünün yüzleri eşkenar üçgendir.
[CH] yüksekliğinin ayağı tabandaki eşkenar üçgenin ağırlık merkezidir.
Düzgün dörtyüzlünün bir kenarı 6 birim olduğundan, yan yüz yükseklikleri birimdir.
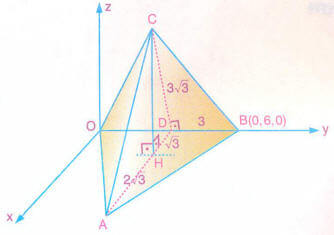
Şekilde,
|OD| = |DB| =3 birim,
|AD| = |CD| = birim,
|HD| = birim olduğundan,
H(, 3, 0) ve A(
, 3, 0) olur.
CHD dik üçgeninde pisagor bağıntısından,
|CH|² = 27-3 = 24
|CH| = birim olduğundan,
C(, 3,
) bulunur.
Düzgün Dörtyüzlünün Alan ve Hacmi
Bir ayrıtının uzunluğu a birim olan düzgün dörtyüzlünün, alanı, birimkare, hacmi ise,
birimküptür.
Bir kenarı a birim olan eşkenar üçgenin alanı, tür. Bir düzgün dörtyüzlüde birbirine eş dört tane eşkenar üçgen olduğundan, alanı,
birimkare olur.
Bir piramidin hacmi taban alanı ile cisim yüksekliğinin çarpımının üçte birine eşittir. Buna göre, taban alanı, , yüksekliği
olan düzgün dörtyüzlünün hacmi,
birimküp olur.
Örnek:
- Bir ayrıt uzunluğu 3 cm olan düzgün dörtyüzlünün alanını ve hacmini bulalım.
Çözüm
- Bir kenarı a = 3 cm olan düzgün dörtyüzlünün alanı,
olur.
- Hacmi ise,
olur.
NOT:
Bir kenarı a birim olan düzgün sekizyüzlünün,
alanı; birimkare
hacmi; birimküp olur.
Düzgün dörtyüzlünün yüksekliği, yani P ve T tepe noktaları arasındaki uzaklık, birimdir.
Örnek:
- Alanı
olan düzgün sekizyüzlünün hacmini bulalım.
Çözüm
Düzgün sekizyüzlünün bir ayrıt uzunluğuna a dersek, alanı olduğundan,
olur.
Bir kenarı 6 cm olan düzgün sekizyüzlünün hacmi,
bulunur.
Düzgün Dörtyüzlü Özellikleri
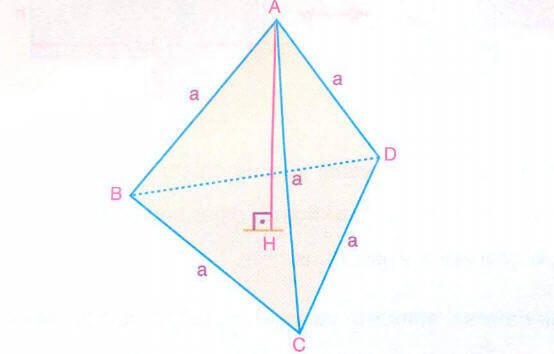
Bir ayrıtının uzunluğu a birim olan bir düzgün dörtyüzlü alalım.
Şekilde, |AD| = a birim ve |DF| = |FC| = birimdir.
AFD dik üçgeninde pisagor bağıntısından veya ACD eşkenar üçgeninin yüksekliğinden,
düzgün dörtyüzlünün yan yüz yüksekliği
birim olur.
Şekilde [BF], BCD eşkenar üçgeninin yüksekliği olduğundan,
birimdir.
H noktası tabanın ağırlık merkezi olduğundan,
birim olur.
AHF dik üçgeninde pisagor bağıntısından,
olduğundan
düzgün dörtyüzlünün cisim yüksekliği
birim olur.
3 yorum
Yeni içerikleri hep takip edeceğim. Gerçekten dopdolu bir sayfa olmuş.Bütün her şey açık ve seçik ortada.
Teşekkür ederiz…
gerçekten çok açıklayıcı. çok başarılı olmuş. takip edeceğim.