Galileo Galilei, serbest düşme ve hareket kanunları ile ilgili hangi çalışmaları yapmıştır? Galileo’nun serbest düşme deney ve açıklaması.

Galileo Galilei
Galileo Galilei ve Serbest Düşme Yasası
Galileo Galilei, 15 Şubat 1564 tarihinde Pisa’da doğdu. Babası Vincenzo Galilei kumaş taciriydi. Ama aynı zamanda döneminin tanınmış bir matematikçisi ve müzik kuramcısıydı. Kepler, Vincenzo’nun armoni ile ilgili kitabını Viyana’dan Graz’a yolculuğu sırasında okumak için yanma almıştı. Galileo Galilei eğitiminin bir bölümünü babasından, bir bölümünü de Floransa yakınındaki Vallombrosa Manastırı’ndan aldı. O günlerde başarı yeteneğe olduğu kadar, himaye edilmeye de dayanırdı. Galileo, Marki Guido Ubaldo del Monte’nin dikkatini çekecek kadar şanslıydı ve koruyucusunun yardımıyla henüz yirmi beş yaşındayken Pisa matematik kürsüsüne atandı. Galileo, kural tanımazlığı ve saldırgan mizacı yüzünden çok önemli düşmanlar edindi. Pisa’nın kısır ve doyumsuz koşullarım terk etmeye pek hevesli olduğundan, 1692’de aynı koruyucunun yardımıyla Padua’da matematik kürsüsüne getirildi.
Kendi geliştirdiği teleskobuyla yaptığı bir dizi ilginç gözlemin sonucunu aktardığı The Starry Messenger (Yıldız Habercisi) kitabının yayımlanmasıyla, 1610 yılında Galileo’nun yıldızı parladı. Kitap, ayın engebeli arazisinin oldukça ayrıntılı bir tasvirini ve asıl önemlisi Galileo’nun Jüpiter’in ayları ile ilgili keşfinin inandırıcı kanıtlarını içeriyordu. Güneş sistemlinde ikinci bir çekim merkezinin varlığım gösteren bu keşif, Galileo’nun başına dertler açtı. Çünkü Padualı Aristocuların Galileo’nun teleskobundan gözlemlemeyi reddettikleri nesneler Jüpiter’in aylarıydı.
İki Büyük Dünya Sistemi Üzerine Diyalog
Galileo, Toskana Grandükünün baş matematikçisi olarak 1610 yılında Floransa’ya geldi. Hemen dikkatleri üzerine çekmeye başladı, devlet ile kilisenin en yüksek makamlarında dost ve hayranlar kazandı. Ayrıca Galileo daha önce Kardinal Bonafeo Barberini olarak tanıdığı Papa VIII. Urban’ın desteğini kazandı. Ama 1632’de Papa’nın karşı çıkmasına karşın, Dialogue on the Two Great World Systems (İki Büyük Dünya Sistemi Üzerine Diyalog) adlı eserini yayımladı. Eserce Galileo ile bir ya da iki arkadaşım temsil eden bir grup bilimadamı, Copernicus’un kuramı ile karşı kuramları tartışıyorlardı.
VIII. Urban bilinmeyen bir nedenden ötürü bu kitabın yayımlanmasına çok öfkelendi ve Galileo’yu yargılanmak üzere Roma’ya gönderdi. Galileo, kitabında dile getirdiği düşünceleri 1633’te geri aldı. Ev hapsine mahkûm edildi ve bilimsel çalışmalarını yayımlaması yasaklandı. Ama o, mahkûmiyeti boyunca, gayret ve azimle Dialogue concerning Two New Sciences (İki Yeni Bilim Üzerine Diyalog) adlı eseri üzerinde Çalışmayı sürdürdü. Bu bölümde belirtilen bütün keşiflerin Yer aldığı bu kitap, doğal olarak İtalya’da ortaya çıkarılamadı; ancak 1638’de Leyden’de Elzevir tarafından yayımlanabildi.
Yaşamının ilk döneminde çocuklarına karşı duygusuzca davranan Galileo, son yıllarında kızıyla yakınlaştı. Böylece yaşlılığında kendisine bakan bir kızı oldu. Galileo 8 Ocak 1642 tarihinde öldü.

Galileo aygıtını gösteriyor. Giuseppe Bezzuoli tarafından yapılmış çağdaş bir duvar resmi. Tribuna de Galileo, Museo Zoologico “La Secola”, Firenze.
Hareket yasaları üzerine ilk çalışmalar: Merton teoremi
Kuşkusuz Galileo’nun deneyleri hareket yasalarıyla ilgili Oxford Merton College’de, 1328’de başlatılan çalışmaların doruk noktasını oluşturdu. O yıllarda Thomas Bradwardine Tractatus de Proportionibus adlı denemeyi tamamlamıştı. Bradwardine’in kinematik (hareket bilimi) sorununa yönelmesi, anlaşıldığı kadarıyla, Merton’un ödüllü üç matematikçisi William Heytesbury (yaklaşık 1310-1380), Richard Swi-neshead (1340’larda Merton’ da) ve John Dumbleton (yaklaşık 1330 ile 1350 arasında Merton’ da) tarafından teşvik edilmişti.
Marshall Clagett’e göre, bu üç bilimadamının matematik çalışmaları, ortaçağ mekanik bilimleri tarihinde, hareket biliminin pek çok temel kavramının gelişmesine önayak olmuştu. Bu çalışmalar, hareketlerarası farkı, hareketin nedenleri ile ilgili kuramı, hareket bilimini, hareket sürecine ve etkilerine ilişkin kuramı, ivme kavramının tam bir formülasyonunu ve hepsinin üzerinde, sabit ivmeli hareketin anlaşılmasının anahtarı olan ortalama hız teoreminin bir kanıtını kapsıyordu. İki merkezi düşünceye sarılmak gerekiyordu: Bir cisim hızlandığında, her an değişik bir hıza sahip oluyordu. Bu, Heytesbury tarafından açıkça tanımlanan anlık hız kavramına başvurmayı gerekli kılıyordu. Ama hareket eden bir cismin aldığı toplam yol ile harcanan toplam zamanı karşılaştırırsak, yalnız ortalama hızı hesaplayabilirdik. Anlık hızın ölçülmesi olanaksızdı, çünkü bunun için cismin anlık bir hızla belirli bir süre hareket ettiğini ve belli bir yol aldığını kabul etmek gerekirdi. Mertonlu matematikçilerin düzgün hızlanan hareketin yasaların bulmalarını mümkün kılan deha patlaması, ivmeli hareket olgusunun ortalama hıza başvurmadan da anlaşılabileceğinin gösterilmesi oldu.
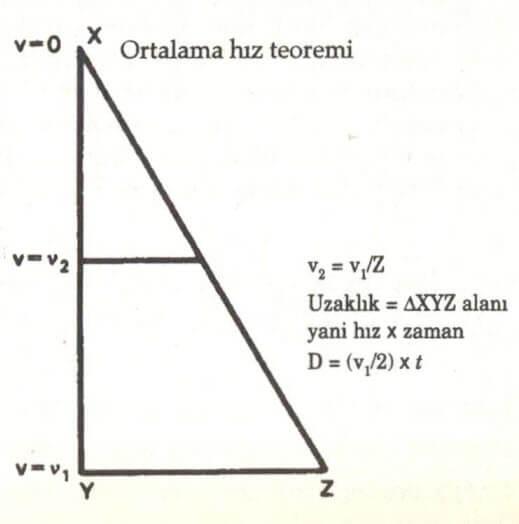
Ortalama hız teoremi neydi?
Düzgün hızlanan bir cisim, birim zaman süresince ortalama hızla alabileceği kadar yol alır. Cismin başlangıçta hareketsiz olduğunu varsayarak olayı basitleştirirsek, teorem geometrik olarak da dile getirilebilir.
Galileo’nun, düzgün hızlanan hareket yasalarının biçimine ilişkin hipotezini doğrudan ya da dolaylı olarak ne ölçüde bu matematiksel analizlerden aldığı, araştırmacıların üzerinde anlaşamadıkları bir konudur. Two New Sciences’da Galileo, deneyi, serbest düşen cisimlerin ivmelerinin yukarıda yorumlanan mantığa uygun davrandığından emin olmak için yaptığını söyler. Burada söz konusu olan yorum ortalama hız teoreminin bir kanıtıdır. Bununla beraber, Galileo’nun notları üzerine bir çalışmasında Stillman Drake, onun 1603 ya da 1604 yılında eğik düzlemde yuvarlanan bir topla deneyler yaptığım, deneyden önce de yasalardan hiç kuşku duymadığını ileri sürmüştür. Olayın aslı ne olursa olsun, burada anlatacağımız deney, kesin biçimi bulunmaya çalışılsa da, bir yasanın varlığının baştan kabulünü gerektirir.
Galileo’nun bir hareket yasasının biçimini deneyle bulması
Galileo, hareketle ilgili matematiksel çalışmayla deneysel çalışmayı titizlikle birbirinden ayırır. Galileo Şöyle diyor: “Herkes rasgele bir hareket biçimi tasarlayıp sonra onun özelliklerini tartışabilir. Biz gerçek doğada olduğu gibi ivmeyle düşen bir kütle tasarlamaya karar verdik … inancımız [ki hep böyle yaparız]deneysel yolla kanıtladığımız özelliklerle uyumlu görünen deney sonuçlarını onaylar.” Dikkat edilmesi gereken ilk şey kütlelerin düşmeye yavaş başlamaları ve hızlarım giderek artırmalarıdır. Yani düşüşün ivmeli olmasıdır. Ağır bir top, yumuşak bir zemine, gittikçe daha yüksekten düşürülerek kolayca denenebilir bu. Top ne kadar yüksekten düşerse, zeminde ona orantılı bir çukur açar.
Ama serbest düşme sırasında, bir kütlenin hareketini kesin olarak gözlemlemek ve ölçmek çok zordu. Galileo bu zorluğu, hareketi bir eğik düzleme taşıyarak ve böylece onu yerçekiminden daha küçük bir ivme altında inceleyerek aştı Ortalama hız teoremine göre alman yol bu sırada harcanan zamanın karesiyle orantılıydı. Yasayla ilgili düşüncelerini ister bu teoremden isterse ilk deneylerden türetmiş olsun, Galileo, alman yolların oranım harcanan zamanların oranıyla karşılaştırmaya girişti.
Deneyde, oluk açılıp cilalandıktan sonra parşömenle kaplanan bir kalas kullanılıyordu. Kalas eğik olarak yerleştirildikten sonra oluk üzerinden bronz bir top yuvarlanacaktı. Deneyin ilk bölümünde, böyle bir dizi deneme için beklenen değişme miktarları, iniş için harcanan zaman, kronometre niyetine nabız tutularak ölçüldü. Belirli bir yükseklikten iniş için harcanan zaman hemen hemen aynı kalıyordu.

Sabit ivmeli hareket için uzaklık ile zaman arasında kurulan kuramsal ilişki, top, kalas uzunluğunun dörtte birinden, sonra yansından, üçte ikisinden vs. yuvarlanarak ve her iniş için harcanan zaman ölçülerek sınandı. Gerçekten de top, kalas boyunun dörtte birine erişmek için, tamamından inmek için gereken zamanın yansım kullandı. Hangi uzaklık seçilirse seçilsin, yüzlerce kez tekrarlanan deneyler sonunda, alman yollar arasındaki ilişkinin, harcanan zamanların kareleri arasındaki ilişkiye benzediği görüldü. Deneylerin son bölümünde zaman, çok büyük bir teknenin dibine yerleştirilen ince bir tüpten akan suyun ağırlığıyla ölçüldü. Bu tekne öylesine büyüktü ki, akan su tüpteki basınçta hissedilir bir değişiklik yapmıyor, böylece suyun akış hızı sabit kalıyordu.
T. Settle, 1961 yılında, Galileo’nun yöntemine olabildiğin’ ce sadık kalarak bu deneyi tekrarladı. Böylece aynı sonuçlan daha mükemmel olarak yeniden elde etmekle kalmadı, Galileo’nun deneylerinin hayal ürünü olduğuna dair bir zamanlar geçerli olan görüşe de son verdi.
Hareket biliminde daha sonraki gelişmeler
Ne var ki Galileo’nun araştırmalarında iki soru yanıtlanmadan kalmıştı. Kütleler niçin sabit ivmeyle düşerler? Yeryüzünde geçerli olan hareket yasaları, yıldızlar ve gezegenler de içinde olmak üzere, evrendeki her kütleye uygulanabilir mi? Newton’un bu sorulardan bazılarına verdiği yanıtlarla bilimadamları 20. yüzyılın başlarına kadar yetinmişlerdi.
Kepler’den sonra Newton, evrende iki kütlenin merkezi arasında birbirini etkileyen kuvvetlerin var olabileceğini düşündü. Bunlar açıklanmayan bir etkinin, yani kütlesel çekimin sonucuydu. Newton, temel ilke olarak kütlesel çekim yasasını önerdi. Bu yasaya göre, herhangi iki kütle arasındaki çekim kuvveti kütlelerin çarpımıyla doğru orantılı, aralarındaki uzaklığın karesiyle ters orantılıdır. Yeryüzünde, bir kütlenin düşmesinde olduğu gibi çok küçük uzaklıklar söz konusuysa, bu kuvvet hemen hemen sabit kalır ve böylece Galileo’nun incelediği sabit ivmeli hareket ortaya çıkar.

Galileo’nun düzeneğinin bir kopyası. Toskana Grandükü için 1775’te yapılmış. Instituto e Museo di Storia della Scienza, Floransa.
Kütle çekim yasası aynı dünya, gezegenlerin güneş etrafında neden döndüğünü açıklıyordu. Bu kütleler, çekim kuvveti olmasa, yörüngelerine teğet bir doğru boyunca hareket edeceklerdi. Ama onlar bir çekim kuvvetinden etkilendiklerinden, etrafında dönecek biçimde ağır kütleye doğru sürükleniyorlardı. Kısacası, sürekli olarak düşüyorlardı. Yörüngesel hareket, doğrusal hareketle sürekli düşmenin bir kütlede dengelenmiş bir karışımıydı. Bu yasa gökyüzünde saptadığımız, daireye benzer yörüngesel hareketleri pek çok durumda açıklar. Aynı yasalar yeryüzünde olduğu gibi yıldızlar arasında da geçerlidir.
Mertonlularca matematiksel analizleri başlatılan ve Galileo tarafından deneysel olarak gösterilen hareket yasaları gerçek dünyaya uygundu. Galileo’dan sonraki yüzyıllarda dikkat ve titizlikle daha saf kavramların tanımlanmasına ve daha gelişkin matematiksel yöntemlerin hazırlanmasına girişildi Enerji ile momentum arasına ayrım kondu ve temel araştırma yöntemi olarak cebir, geometrinin yerini aldı. Bu gelişmeler çok daha karmaşık hareketleri ve çok daha gelişkin yapılan matematiksel olarak ele almamıza olanak sağladı.
Mekanik kanunlarının doğaya uygunluğunu sınamak üzere çok daha gelişmiş makineler, örneğin Atwood makinesi, ancak 19. yüzyılda geliştirildi.
Galileo’nun deneyinde, düşüncede geliştirilen bir kavramsal sistemin gerçek dünyaya uygunluğunun deneyle sınanmasının çok saf bir örneğini görürüz. Bu deneyin mantığım yalnızca tümevarımla ya da deneme-yanılma yöntemiyle açıklamak olanaklı değildi.