Lineer Bağımlı ve Lineer Bağımsız Vektörler

12. sınıf geometri dersi, lineer bağımlı ve lineer bağımsız vektörler konu anlatımı, örnekler. Lineer bağımlı ve bağımsız vektörler özet.

Lineer Bağımlı ve Lineer Bağımsız Vektörler

Uzayda doğrultuları aynı olan iki vektör lineer bağımlıdır.

Yani biri diğerinin bir reel sayı katı olarak yazılabilir. Uzayda,

$\displaystyle \overrightarrow{a}$ ve $\displaystyle \overrightarrow{b}$ vektör, k bir reel sayı olmak üzere,

$\displaystyle \overrightarrow{a}=k.\overrightarrow{b}$ ise

$\displaystyle \overrightarrow{a}$ ve $\displaystyle \overrightarrow{b}$ vektörleri lineer bağımlıdır.

Örnek:

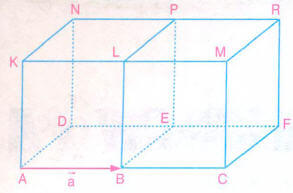
Şekildeki, $\displaystyle \overrightarrow{a}=\overrightarrow{AB}$ vektörü ile lineer bağımlı olan vektörleri bulalım.

Şekil üzerinde $\displaystyle \overrightarrow{AB}$ vektörü ile lineer bağımlı olan yani bir reel sayı katı olarak yazılabilen vektörler
$\displaystyle \overrightarrow{AC},\overrightarrow{DE},\overrightarrow{DF},\overrightarrow{FE},\overrightarrow{KL},\overrightarrow{RN},\overrightarrow{ML}$ gibi vektörlerdir.

NOT:

Uzayda, doğrultuları farklı olan iki vektör lineer bağımsızdır. Yani biri diğerinin katı olarak yazılamaz.

Tanım

Uzayda, $\displaystyle \overrightarrow{u},\overrightarrow{v},\overrightarrow{w}$ vektörleri verildiğinde, $\displaystyle \overrightarrow{w}={{a}_{1}}\overrightarrow{u}+{{a}_{2}}\overrightarrow{v}$ olacak şekilde $\displaystyle {{a}_{1}},{{a}_{2}}\in R$ bulunabiliyorsa bu üç vektöre lineer bağımlı, bulunamıyorsa lineer bağımsız vektörler denir.

Uzayda, lineer bağımlı üç vektör düzlemseldir.

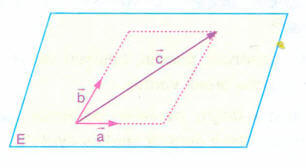
Uzayda, herhangi üçü aynı düzlemde bulunmayan dört vektör lineer bağımsız olamaz. Yani biri diğerleri cinsinden yazılır.

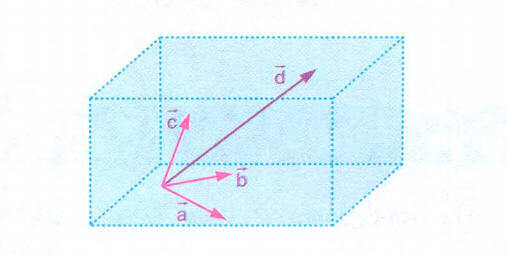
Uzayda, doğrultuları farklı iki veya daha fazla vektör verildiğinde, vektörler başlangıç noktaları aynı olacak şekilde taşınır ve birinin diğerleri cinsinden gösterilip gösterilemeyeceği sorgulanır.

Örnek

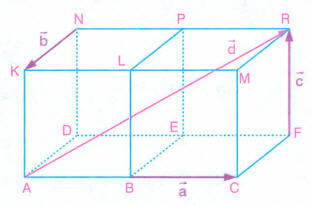
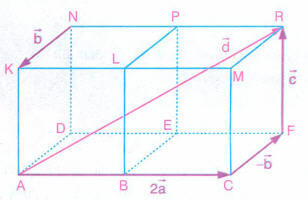
Yukarıda, iki küpün birleştirilmesiyle oluşan şekilde,

$\displaystyle \overrightarrow{d}=\overrightarrow{AR}$ vektörünün $\displaystyle \overrightarrow{a},\overrightarrow{b},\overrightarrow{c}$ vektörlerinin lineer bileşimi şeklinde yazılışını bulalım.

$\displaystyle \overrightarrow{a}$ vektörünü $\displaystyle \overrightarrow{d}$ vektörünün başlangıç noktasına taşıyıp 2 ile çarpalım. Uç uca ekleme yöntemiyle $\displaystyle \overrightarrow{-b}$ vektörünü ve $\displaystyle \overrightarrow{c}$ vektörlerini toplarsak,