Newton’un hareket yasaları, 1. eylemsizlik yasası, 2. dinamiğin temel yasası ve 3. eylemsizlik yasası, formülleri, f=ma bağıntısı sonuçları.
NEWTON’UN HAREKET YASALARI

I. YASA : EYLEMSİZLİK YASASI
Bir cisme hiç bir kuvvet etkimiyorsa ya da etkiyen kuvvetlerin bileşkesi sıfırsa bu cismin hızında hiç bir değişiklik olmaz.
- Bileşke kuvvete
diyecek olursak, bu ifade,
biçimini alır. Bu ifadenin bir başka anlamı da şudur : Cisme etkiyen kuvvetlerin bileşkesi sıfırsa cisim düzgün doğrusal hareket yapar. Ya da tersine, cisim düzgün doğrusal hareket yapıyorsa bu cisme ya hiç bir kuvvet etkimiyor, ya da etkiyen kuvvetlerin bileşkesi sıfırdır.
II. YASA : DİNAMİĞİN TEMEL YASASI
Birinci yasa, bileşke kuvvet sıfırsa hızın değişmediğini söylüyordu. Hızın değişmemesiyse ivmenin sıfır olması demektir. Demek, ki bileşke kuvvet sıfır olunca ivme sıfır olmaktadır. Bu sonuç bize ivmenin kuvvetle doğru orantılı olabileceğini düşündürür. Gerçekten de bu böyledir. Newton’un ikinci hareket yasası bu ilişkiyi anlatır:
Bir cisme etkiyen kuvvetlerin bileşkesi sıfır değilse cisim, mutlaka ivmeli bir hareket yapar ve ivme her an bileşke kuvvetle doğru orantılıdır.
İvme, bileşke kuvvetle doğru orantılı olduğuna göre bu iki niceliğin arasındaki oran sabit kalmalıdır. Yapılan deneyler, aynı bir cisim için bu oranın değişmediğini göstermiştir. Deneyin konusu olan cisim değişince de oranın başka bir sabite eşit olduğu gözlenmiştir.
Deneylerde bu sabit, bizim ağır diye nitelediğimiz cisimler için büyük, hafif diye nitelediğimiz cisimler içinse küçük çıkmıştır. Acaba kütleyle bir ilgisi olabilir mi diye düşünülmüş, ölçme yapıldığında da kütleye tam eşit olduğu görülmüştür. O halde bileşke kuvvetin ivmeye oranı cismin kütlesine eşittir.
Bu basit bağıntı, dinamiğin temel formülü adını alır. Gerçekten de elle tutulur, gözle görülür bir çevrede bu bağıntıya uymayan hareket yoktur, Kaldı ki atomik boyutlarda bile hareketler, bir çok durumda, bu bağıntıyla açıklanabilmektedir.
BAĞINTISINDAN ÇIKAN SONUÇLAR
I. Hareketin nedeni kuvvettir. İvmeyse hareketin ta kendisidir. Kütle, hareket eden cisimdeki madde miktarıdır. F=m.a bağıntısı bu üç niceliği birbirine bağladığı için çok önemlidir. Kuvvet nedense, ivme bir sonuçtur. Dolayısıyla bu bağıntı, neden-sonuç ilişkisinin en yalın bir matematiksel anlatımıdır.
II. İvmenin yaratıcısı bileşke kuvvettir. İvmenin kendisiyse hareketin belirleyicisidir. Yani ivmeye bakarak hareketin nasıl olacağını kestirmek olasıdır. O halde cisme etkiyen tüm kuvvetlerin bileşkesini bulduk mu, ivmeyi, dolayısıyla hareketin nasıl oluşacağını bulmuş oluruz. Diyelim ki bileşke kuvvet yön ve değer olarak sabit. İvme de sabit olur. Eğer bu arada bileşke kuvvetin yönü hız ile aynı ise cisim sürekli hız kazanır ve düzgün hızlanan doğrusal hareket yapar. Bileşke kuvvet hıza ters yöndeyse bu kez de düzgün yavaşlayan doğrusal hareket yapar. Ya da bileşke kuvvet her an hıza dik kalıyorsa saptırıcı etki yapar ve cisim çember üzerinde dolanır. Görülüyor ki, bileşke kuvvetin özeliklerinin bilinmesi cismin ne tür hareket yapacağının anlaşılması demek oluyor.
Hareket eden şey tek cisim değil de cisimler grubuysa böyle bir gruba sistem diyoruz. F = m.a bağıntısındaki kütle de artık tek cismin değil, sistemin kütlesidir. Yani harekete katılan tüm kütledir. F de sisteme dışarıdan etkiyen kuvvetlerin bileşkesidir. Bir sistemi oluşturan parçalar arasındaki karşılıklı etkileşim kuvvetleri, sistemin iç kuvvetleri adını alır ve harekete hiç bir etkileri yoktur. Bileşke kuvveti alırken daima dış kuvvetlerin bileşkesini alırız. Zaten iç kuvvetlerin bileşkesi sıfır olur. Örneğin bir otobüsün içindeki yolcular birbirini itip kaksalar, otobüsün hareket durumunda hiç bir değişiklik olmaz.
III. bağıntısında kuvvet ve ivme birer vektör, kütleyse pozitif bir skalerdir. Bir vektör pozitif bir skalerle çarpılınca, bu vektörle aynı yönde yeni bir vektör elde edilir. O halde
ile
aynı yöndedir. Bu nedenle deriz ki : Her kuvvet kendi yönünde ivme yaratır.
İvme Hesabı
IV. F = m.a bağıntısına göre mademki kuvvet, kütleyle ivmenin çarpımına eşittir; kuvvetin birimi de kütle birimiyle ivmenin biriminin çarpımı olacaktır :
Kuvvet = Kütle x ivme
Kuvvet birimi = Kütle birimi x ivme birimi
Newton = Kg x m/s²
V. Cisimlerin ağırlığı da F=m.a bağıntısından hesaplanabilir. Ağırlık yerçekimi kuvvetidir, öyleyse, yerçekiminin yarattığı ivmeyi kütleyle çarparsak ağırlığı bulmuş oluruz.
- Ağırlık = Kütle x Yerçekimi ivmesi
- g nin yeryüzündeki ortalama değeri 9,8 m/s² dir.
III. YASA : ETKİ-TEPKİ YASASI
Roketler, havai fişekler, yerde zıplayan bilyeler, geri tepen silahlar, kendi kendine dönen bahçe fıskiyeleri, tepkili uçaklar, mürekkep balıkları… Tüm bu örnekler, etki-tepki yasasına göre çalışan cisim ya da sistemlerdir. Örneğin yere düşen bir bilye,yerden bir tepki görerek geri sıçrar. Bilye,yere değdiği andan itibaren yere bir kuvvet uygulamaya başlar. Bu “etki” dir. Yer de bilyeye bir kuvvet uygular. Bu da “tepki” dir. Bilyeyi geri sıçratan kuvvet budur.
Roketin yakıtı ateşlenince kimyasal tepkimeden çıkan ısı, gaz kütlesini basınçla dışarı atar. Basınç ‘nedeniyle gaz taneciklerine uygulanan kuvvetler birer etkidir. Gaz tanecikleri de roket gövdesine bir kuvvet uygularlar. Bunlar da tepkidir. Bu tepki kuvvetleri roketin gövdesini yukarı kaldırır..
Masa üzerinde duran bir kitap, ağırlığı nedeniyle masa yüzeyini aşağı doğru bastırır. Masa da kitaba yukarıya doğru bir kuvvet uygular. Kitabın masaya uyguladığı kuvvet etki, masanın kitaba uyguladığı kuvvetse tepkidir. Örnekleri çoğaltmak olası. Hepsinde de bir etkiye karşılık mutlaka bir tepki vardır. Bu nedenle üçüncü yasanın ifadesi şöyledir :
Her etki, kendisine eşit değerde ve ters yönde bir tepki yaratır.
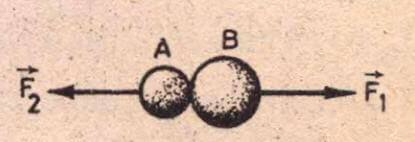
Şekildeki gibi, bir A cismi B cismine Fx kuvvetini uygularsa, B cismi de A ya F2 kuvvetini uygular. Bu kuvvetler arasında her zaman,
bağıntısı vardır. Etki ile tepki eşit ve ters yönlü oldukları halde bileşikleri sıfır etmez. Zaten bileşikleri alınamaz. Çünkü aynı cisme etkimiyorlar. İki kuvvetin bileşkesinin alınabilmesi için aynı noktaya ya da aynı bir cisme etkimeleri gerekir. Bunu gözönünde bulundurarak etkiyle tepkinin bileşkesini bulmaya kalkışmayalım.