Süreklilik nedir? Süreklilik konu anlatımı, özellikleri, hesaplanması, örnek sorular ve çözümleri.
SÜREKLİLİK:
Tanım: olmak üzere
fonksiyonu tanımlansın. f(x) fonksiyonu için:
ise f(x) fonksiyonu
noktasında süreklidir, denir.
Fonksiyon noktasında sürekli değilse bu noktada süreksizdir denir.
ÖZELLİKLER:
1) f(x) fonksiyonunun noktasında limiti yoksa bu noktada süreksizdir.
2) f(x)in da limiti varsa bu noktada sürekli olmak zorunda değildir.
3) f(x), da limitli ve bu noktada tanımlı ise x=Xq da sürekli olmak zorunda değildir.
4) f(x), da sürekli ise bu noktada limiti vardır.
5) f(x), da süreksiz ise bu noktada limitsiz olmak zorunda değildir.
6) f(x), da tanımlı değilse bu noktada süreksizdir.
7) f(x), (a, b) aralığının her noktasında sürekli ise (a,b) aralığında süreklidir denir.
8) (a,b) aralığında tanımlı bir f(x) fonksiyonu x=a ve x=b de sürekli değildir.
ÖRNEK:
fonksiyonunun sürekli olduğu kümeyi yazınız.
ÇÖZÜM:
fonksiyonu
noktalarında tanımlı olmadığından sürekli de değildir. Sürekli olduğu noktalar kümesi S= R-[±2] olur.
ÖRNEK:
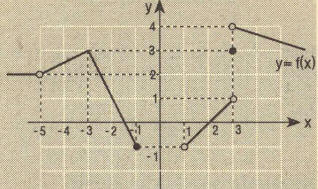
y=f(x) fonksiyonunun grafiği veriliyor. Buna göre fonksiyon;
a) x= -5 de süreksiz (limit ve fonksiyon değeri farklı)
b) x= -3 de sürekli
c) x= -1 de süreksiz (limit yok)
d) x=1 de süreksiz, (limit yok)
e) x=2 de sürekli
f) x=3 de süreksiz (limit yok)
ÖRNEK:
fonksiyonu x=2 noktasında sürekli ise m+p toplamı nedir?
ÇÖZÜM:
f(x), x=2 de sürekli ise
olmalıdır.
bulunur.
olur.