Üçgenin Kenar Uzunlukları Arasındaki İlişki

Bir üçgende kenar uzunlukları diğer kenarlarla olan ilişkisi, açı ile olan ilişkisi, bağıntılar ve özelliklerin örnekli açıklamaları

AÇI-KENAR BAĞINTILARI

1″)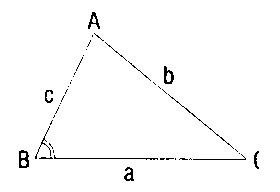

Bir üçgende büyük açı karşısında büyük kenar, küçük açı karşısında küçük kenar bulunur.

2)

Bir üçgenin iki kenarından uzun olanın karşısındaki açının ölçüsü, kısa olan kenarın karşısındaki açının ölçüsünden daha büyüktür.

3)

Bir üçgende iki kenar eş ise, bu iki kenarın karşısındaki açılar da eşittir.

4)

5)

6)

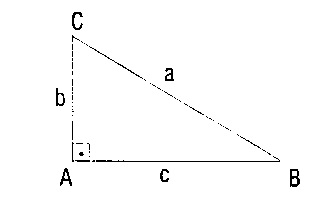
KENAR İLİŞKİLERİ – ÜÇGEN EŞİTSİZLİĞİ

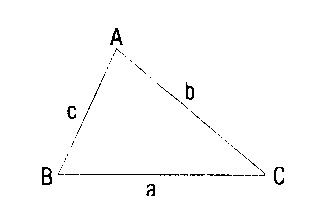
1) latex \displaystyle \left| a-c \right|<b<a+c$

Bir üçgende bir kenar uzunluğu diğer kenar uzunlukları toplamından küçük, farklarının mutlak değerinden büyüktür.

2)

$latex \displaystyle \left. a{{V}_{b}}>{{V}_{c}}$

$latex \displaystyle \left. a{{n}_{b}}>{{n}_{c}}$

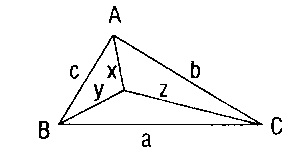
3)

Bir üçgenin içindeki bir noktanın köşelere olan uzaklıklarının toplamı, üçgenin çevresinden küçük ve yarı çevresinden büyüktür.