Üçgenlerde Alan Bağıntıları

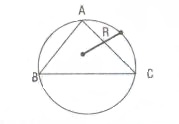
Üçgenin alanı nasıl hesaplanır? Üçgenlerde alanla ilgili bağıntılar, formüller, örnekli anlatım.

Üçgenlerde Alan Bağıntıları

1) Dik üçgenin alanı, dik kenar uzunlukları çarpımının yansına eşittir.

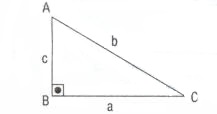
ucgende-alan-1

$\displaystyle A\left( \overset{\Delta }{\mathop{ABC}}\, \right)=\frac{1}{2}a.c$

2) Üçgenin alanı, herhangi bir kenar uzunluğu ile bu kenara ait yüksekliğin çarpımının yarısına eşittir.

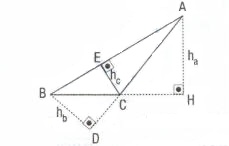
ucgende-alan-2

$\displaystyle A\left( \overset{\Delta }{\mathop{ABC}}\, \right)=\frac{1}{2}a.{{h}_{a}}=\frac{1}{2}b.{{h}_{b}}=\frac{1}{2}c.{{h}_{c}}$

ÖRNEK:

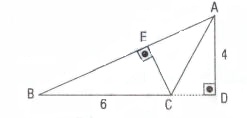
ucgende-alan-3

Yukarıdaki ABC üçgeninde [AD], [CE] yükseklikler |AB| = 8, |BC| = 6 |AD| = 4 ise |CE| nin değeri kaçtır?

$\displaystyle A\left( \overset{\Delta }{\mathop{ABC}}\, \right)=\frac{1}{2}a.{{h}_{a}}=\frac{1}{2}6.4=12$

$\displaystyle A\left( \overset{\Delta }{\mathop{ABC}}\, \right)=\frac{1}{2}c.{{h}_{c}}$ bilinenler yerine konursa,

$\displaystyle 12=\frac{1}{2}.8.{{h}_{c}}\Rightarrow {{h}_{c}}=3$

3) Kenar uzunlukları a,b,c olan üçgenin alanı:

a + b + c = 2u olmak koşulu ile

$\displaystyle A\left( \overset{\Delta }{\mathop{ABC}}\, \right)=\sqrt{u\left( u-a \right)\left( u-b \right)\left( u-c \right)}$

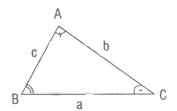
4) Kenar uzunlukları a,b,c ve açılarının ölçüleri A,B,C olan üçgenin alanı; herhangi iki kenarı ile bu kenarlar arasındaki açının sinüsü çarpımı yarısına eşittir.

ucgende-alan-4

$\displaystyle A\left( \overset{\Delta }{\mathop{ABC}}\, \right)=\frac{1}{2}bc\sin A=\frac{1}{2}ac\sin B=\frac{1}{2}ab\sin C$

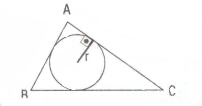
5) Kenar uzunlukları a,b,c ve iç teğet çemberinin yarıçapı r olan üçgenin alanı; Üçgenin çevresinin yarısı ile iç teğet çemberin yarıçapı çarpımına eşittir.

ucgende-alan-5

$\displaystyle 2u=a+b+c$

$\displaystyle A\left( \overset{\Delta }{\mathop{ABC}}\, \right)=u.r$

6) Kenar uzunlukları a,b,c ve çevrel çemberinin yarıçapı R olan üçgenin alanı; kenarları çarpımının çevrel çemberin yarıçapının dört katına bölümüne eşittir.

ucgende-alan-6