Son Yazılar :
NKFUCOM
NKFUCOM

Dik Dairesel Koninin Hacmi Hesaplanması

0
By on Matematik
Advertisement

Dik dairesel koninin hacmi nasıl hesaplanır? Dik dairesel koninin hacim formülü, örnek soru ve çözümlerle hesaplanması.

Dik Dairesel Koninin Hacmi

Dairesel koninin hacmi,

piramidin hacminde olduğu gibi taban alanı ile yüksekliğinin çarpımının üçte birine eşit olur.

Taban yarıçapı r,

yüksekliği h olan bir dairesel koninin hacmi,

V = 1/3 * Taban Alanı * Yükseklik

Advertisement

\displaystyle V=\frac{1}{3}.\pi {{r}^{2}}.h

Örnek:

Taban yarıçapının uzunluğu 8 cm, ana doğrusunun uzunluğu 17 cm olan dik dairesel koninin alan ve hacmini bulalım.

Çözüm

Koni

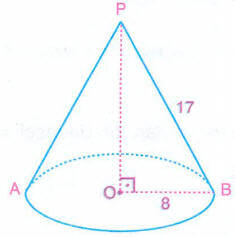
POB dik üçgeninde,

|PB| = 17 cm,

Advertisement

|OB| = 8 cm dir.

(8-15-17) dik üçgeninden,

|PO| = 15 cm olur.

\displaystyle Alan=\pi {{r}^{2}}+\pi r.\ell

\displaystyle Alan=\pi {{8}^{2}}+\pi 8.17

\displaystyle Alan=64\pi +136\pi =200\pi cm² olur.

\displaystyle Hacim=\frac{1}{3}\pi {{.8}^{2}}.15=320\pi cm³

Örnek:

Koni

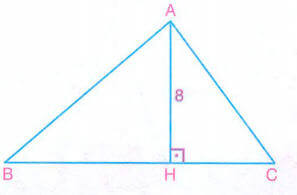
ABC bir üçgen [AH] ⊥ [BC] |AH| =8 cm
|BC| =12 cm

Şekildeki ABC üçgeninin BC kenarı etrafında 360° döndürülmesi ile elde edilen cismin hacmini bulalım.

Çözüm

Advertisement

ABC üçgeninin BC kenarı etrafında döndürülmesi ile tabanları çakışık iki adet koni elde edilir.

Koni

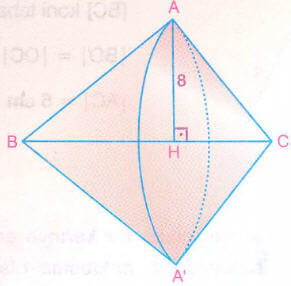
Bu konilerin toplam hacmi, tabanının yarıçapı 8 cm ve yüksekliği 12 cm olan koninin hacmine eşit olur.

\displaystyle Hacim=\frac{1}{3}\pi {{.8}^{2}}.12=256\pi cm³

Örnek

Koni

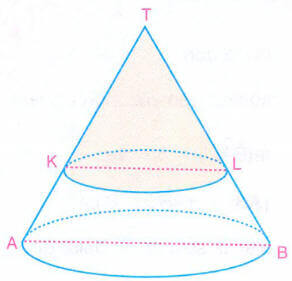
Şekildeki koni tabana paralel bir düzlemle kesiliyor.

|TL| = 2|LB|

Üstteki küçük koninin hacmi 16 cm3 olduğuna göre, alttaki kesik koninin hacmini bulalım.

Çözüm

Üstteki küçük koni ile tüm koni benzerdir. Hacimlerinin oranı benzerlik oranının küpüne eşittir.

\displaystyle {{\left( \frac{2}{3} \right)}^{3}}=\frac{8}{27}

Advertisement

Yani üstteki koninin hacmi 8x ise,

tüm koninin hacmi 27x ve

alttaki kesik koninin hacmi 27x – 8x = 19x olur.

8x = 16
x = 2 ise
19x = 19 * 2 = 38 cm³ olur.

Örnek:

Koni

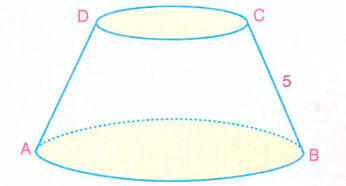
Yukarıdaki kesik koni bir dik koninin tabana paralel bir düzlemle kesilmesiyle elde ediliyor.

Kesik koninin alt taban yarıçapı 6 cm, üst taban yarıçapı 3 cm ve |BC| = 5 cm olduğuna göre, hacmini bulalım.

Çözüm

Koni

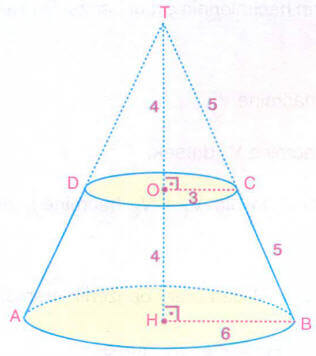
Kesik koniyi tam koniye tamamlarsak TOC üçgeni ile THB üçgeni benzer olur.

Benzerlik oranı, \displaystyle \frac{\left| OC \right|}{\left| HB \right|}=\frac{3}{6}=\frac{1}{2}

Advertisement

Buradan,

\displaystyle \left| TC \right|=\left| CB \right|=5cm
\displaystyle \left| TO \right|=\left| OH \right|=4cm

Büyük koninin hacmi = \displaystyle \frac{\pi .{{r}^{2}}.h}{3}=\frac{\pi {{.6}^{2}}.8}{3}=96\pi cm³

Küçük koninin hacmi = \displaystyle \frac{\pi .{{r}^{2}}.h}{3}=\frac{\pi {{.3}^{2}}.4}{3}=12\pi  cm³

Kesik koninin hacmi = \displaystyle 96\pi -12\pi =84\pi  cm³


Leave A Reply