Osiloskop Konu Anlatımı

Osilosop nedir? Osiloskop nasıl çalışır,formülleri, özellikleri,fizik osiloskop konu anlatımı.

OSİLOSKOP

Sıcak bir fitilden elektronların salınması (termoiyonik salınma) olayının pratikte bir çok uygulama yerleri olup, bunlardan en önemlisi elektron tabancasıdır. Bir elektron tabancası Şekil: 6-31 de olduğu gibi; iyi bir boşluk ortam sağlayan cam tüp, katot olarak kullanılan sıcak fitil ve içinde küçük bir delik bulunan pozitif yüklü (anot) metal silindirden oluşmuştur.

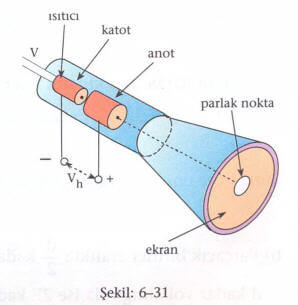
yuklu-tanecikler-sekil-6-31

Sıcak fitilden çıkan elektronların çoğu, Vh hızlandırma gerilimi altında hızlandırılarak silindire (anot) çarpıp kalırlarsa da, bir kısmı delikten geçip bir demet halinde, fluoresan madde kaplı ekranın ortasına çarparak parıldama yaparlar.

Elektron tabancasından ince bir demet halinde çıkan elektronlar, düşey ve yatay saptırıcı paralel levhalar arasında ilerleyerek fluoresan ekranda başka bir noktaya çarpar. Bu noktanın yeri, yatay ve düşey metal levhaların yüklenme çeşidine ve gerilim büyüklüğüne bağlı olarak değişir. Bu yüzden osiloskop potansiyel farklarını (gerilim) ölçmek için voltmetre olarak kullanılabilir.

Şimdi elektron tabancasından çıkan elektronların, saptırıcı levhaları geçtikten sonra, ekrandaki sapma miktarının bağlı olduğu büyüklükleri bulalım.

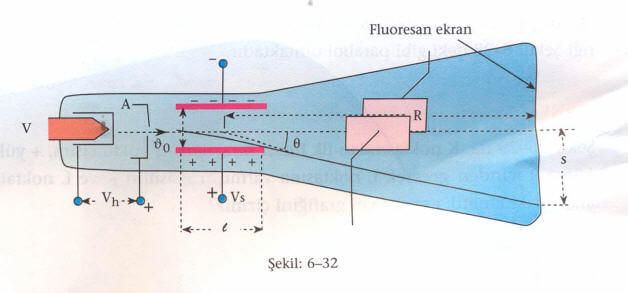
yuklu-tanecikler-sekil-6-32

Şekil-6-32 de, $\displaystyle \tan \theta =\frac{S}{R}$ ve yüklü taneciklerin düzgün elektrik alandaki yörüngeleri bölümünden,

$\displaystyle \tan \theta =\frac{q.{{V}_{s}}.l}{m.d.\vartheta _{0}^{2}}$

eşitlikleri kullanılarak,

$\displaystyle S=\frac{e.l.R.{{V}_{s}}}{m.d.\vartheta _{0}^{2}}$

olur. Fitilden çıkan elektronların, hızlandırma bölgesi sonundaki $\displaystyle {{\vartheta }_{0}}$ hızı,

$\displaystyle e.{{\vartheta }_{h}}=\frac{1}{2}.m.\vartheta _{0}^{2}$

$\displaystyle \vartheta _{0}^{2}=\frac{2.e.{{V}_{h}}}{m}$

değeri S’de yerine yazılarak.

$\displaystyle S=\frac{e.l.R.{{V}_{s}}}{m.d.\frac{2.e.{{V}_{h}}}{m}}$

$\displaystyle S=\frac{1}{2}.\frac{{{V}_{s}}}{{{V}_{h}}}.\frac{l}{d}.R$

bulunur. Eşitlikten görüldüğü gibi sapma miktarı $\displaystyle \frac{e}{m}$ oranına bağlı değildir.

Osiloskop voltmetre olarak kullanıldığında, ekrandaki 1 cm lik sapma için saptırıcı levhalar arasına uygulanan gerilime voltmetrenin duyarlılığı denir. Bu duyarlılık ayrıca hızlandırıcı gerilime (Vh) de bağlıdır.

e / m NİN TAYİNİ

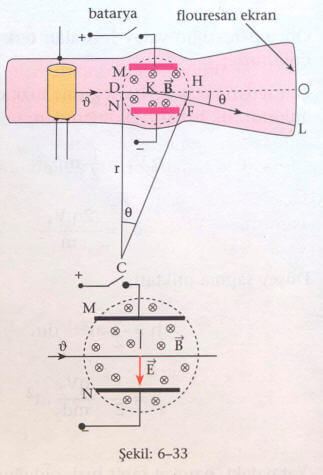
yuklu-tanecikler-sekil-6-33

M ve N metal levhaları arasına Şekil: 6-33 deki gibi sayfa düzlemine dik -B magnetik alan uygulanarak $\displaystyle \frac{e}{m}$ yi ölçmek için elektron tabancasından elde edilen elektronların, O dan L ye gitmesi sağlanır. Metal levhalar bataryaya bağlanıp, gerilimin belli bir değerinde elektronların L den O ya gelmesi sağlanır. Düzgün magnetik alan içerisine dik giren elektrona etkiyen magnetik kuvvet $\displaystyle F=e.\vartheta .B$ olup, bu kuvvet elektronu r yarıçaplı yörüngede dönmeye zorlayacaktır. Dairesel hareket yapan elektronun merkezcil kuvveti de magnetik kuvvete eşit olacaktır.

$\displaystyle e.\vartheta .B=\frac{m.{{\vartheta }^{2}}}{r}$ den,

$\displaystyle \frac{e}{m}=\frac{\vartheta }{B.r}$

olur. DHC üçgeninde $\displaystyle \tan \theta =\frac{\left| DH \right|}{r}$ , KOL üçgeninde ise $\displaystyle \tan \theta =\frac{\left| OL \right|}{\left| OK \right|}$ olacağından;

$\displaystyle \frac{\left| DH \right|}{r}=\frac{\left| OL \right|}{\left| OK \right|}$

$\displaystyle r=\frac{\left| OK \right|.\left| DH \right|}{\left| OL \right|}$

olarak bulunur.

M ve N saptırıcı paralel levhaları bataryanın (+) ve (-) kutuplarına bağlanarak oluşturulan düzgün E elektrik alan şiddeti ile buna dik B magnetik alan şiddeti ayarlanarak elektron demetinin, ekranın O noktasına çarpması sağlanır. Bu durumda elektrona etkiyen elektrik ve magnetik kuvvetler eşit ve zıt yönlü olacağından,

$\displaystyle e.E=e.\vartheta .B$ den

$\displaystyle \vartheta =\frac{E}{B}$ olur.

Ölçülen $\displaystyle \vartheta$ ve r değerleri ile bilinen B değeri $\displaystyle \frac{e}{m}=\frac{\vartheta }{B.r}$ bağıntısında yerine konularak, elektron için buradan $\displaystyle \frac{e}{m}$ oranı bulunur.