Kinetik enerji nedir, nasıl hesaplanır? Kinetik enerji formülleri, denklemi, teoremi açıklaması ve hesaplanması.
KİNETİK ENERJİ (Hareket enerjisi)
Bir cisme hız kazandırmak için gerekli kuvvetin yaptığı işe kinetik enerji denir. Hızı v, kütlesi m olan bir cismin kinetik enerjisi,
ile hesaplanır.
KİNETİK ENERJİ TEOREMİ (İş-enerji teoremi)
Bir cisme etkiyen net kuvvetin yaptığı iş, o cismin kinetik enerjisindeki değişime eşittir.
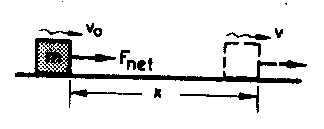
Bunun ispatı kolaydır: Kütlesi m olan bir cisim v0 hızıyla giderken bileşke Fnet kuvveti etkimeye başlamış olsun. Bu kuvvetin etkisiyle cismin, x yolunu aldığında v hızına ulaşmış olduğunu kabul edelim. F kuvvetinin x yolu boyunca yaptığı iş,
olacaktır. Dinamiğin ikinci yasasına göre
olacağından
olur. İvme yerine Δv/ Δt, alınan yol yerine vort . Δt yazılırsa
elde edilir. Burada da ve
yazılarak
bulunur. Burada mv²/2 terimi cismin v hızındaki kinetik enerjisini, yani son kinetik enerjisini, mvo²/2′ terimi de ilk kinetik enerjisini ifade eder. O halde
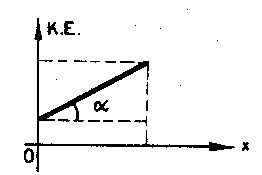
olur. Net kuvvet hızlandırıcıysa, cismin kinetik enerjisindeki değişim artış biçiminde olur. Net kuvvet ilk hıza (hareket yönüne) ters yöndeyse cisim hız kaybına uğrar ve kinetik enerjideki değişim azalış biçiminde olur. Ayrıca bu bağıntıya göre, Şekildeki gibi, enerji-yol grafiğinin eğimi net kuvveti verir. Yani grafikteki a açısının tanjantı net kuvvete eşit olur. Grafiğin altındaki alanın bir anlamı yoktur.
4 yorum
Güzel bir açıklama. Teşekkürler
Vort u yazarken eksiyi kullanınca bir afalladım ancak aşağı kısımda düzeltilip işleme devam edilmiş. 🙂
Heryerde böyle güzel açıklama bulunmuyor teşekkürler
Güzel açıklama ama neden 2 yi getirdiğinizi hala anlamadım
Tebrikler ve teşekkürler. Çok güzel açıklamışsınız.