Matrislerde Çarpma İşlemi

Matrislerde çarpma işlemi nasıl yapılır? Matrislerin çarpımı, örnekli anlatımı.

Matrislerde Çarpma İşlemi

$\displaystyle A={{\left[ {{a}_{ij}} \right]}_{mnx}}$ ve $\displaystyle B={{\left[ {{b}_{ij}} \right]}_{nxp}}$ matrisleri verilmiş olsun. A ile B nin çarpımı;

$\displaystyle {{c}_{ij}}=\sum\limits_{k=1}^{n}{{{a}_{jk}}}.{{b}_{kj}}$ olan $\displaystyle C={{\left[ {{c}_{ij}} \right]}_{mxp}}$ matrisine denir.

C = A.B biçiminde gösterilir. A ve B matrislerinin çarpımlarının tanımlı olabilmesi için A nın sütun sayısının, B nin satır sayısına eşit olması gerekir.

A.A = A², AA² = A³ ….

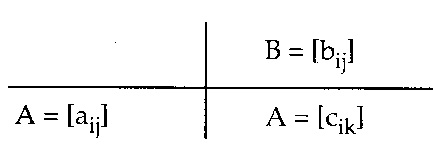
Falk Şeması: Yukarıda verilen A ve B matrislerinin çarpımı olan C matrisini, aşağıdaki verilen ve Faik şeması denilen şema ile bulmak mümkündür.

matris-carpma-1

ÖRNEK:

$\displaystyle A={{\left( \begin{matrix} 2 & -1 & 3 \\ 4 & 0 & 1 \\ \end{matrix} \right)}_{2x3}}$

$\displaystyle B={{\left( \begin{matrix} 5 & -1 \\ 0 & 4 \\ -3 & 2 \\ \end{matrix} \right)}_{3x2}}$

matrsilerinin çarpımını bulun.

ÇÖZÜM

Falk şemasından faydalanarak yapalım.

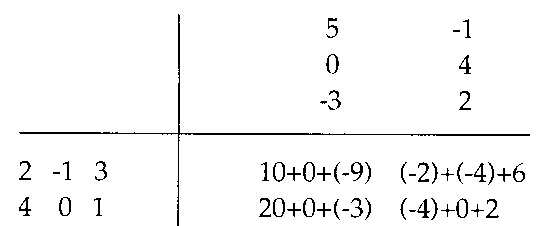
matris-carpma-2

$\displaystyle C=\left( \begin{matrix} 1 & 0 \\ 17 & -2 \\ \end{matrix} \right)$ bulunur.

ÖRNEK

$\displaystyle A=\left( \begin{matrix} 1 & -3 \\ 0 & 1 \\ \end{matrix} \right)$ ise A¹⁵ çarpımını bulunuz.

ÇÖZÜM

$\displaystyle A.A={{A}^{2}}=\left( \begin{matrix} 1 & -3 \\ 0 & 1 \\ \end{matrix} \right)\left( \begin{matrix} 1 & -3 \\ 0 & 1 \\ \end{matrix} \right)$

$\displaystyle {{A}^{2}}=\left( \begin{matrix} 1 & -6 \\ 0 & 1 \\ \end{matrix} \right)=\left( \begin{matrix} 1 & 2.(-3) \\ 0 & 1 \\ \end{matrix} \right)$

$\displaystyle {{A}^{3}}=\left( \begin{matrix} 1 & -6 \\ 0 & 1 \\ \end{matrix} \right)\left( \begin{matrix} 1 & -3 \\ 0 & 1 \\ \end{matrix} \right)=\left( \begin{matrix} 1 & -9 \\ 0 & 1 \\ \end{matrix} \right)$

$\displaystyle {{A}^{3}}=\left( \begin{matrix} 1 & 3(-3) \\ 0 & 1 \\ \end{matrix} \right)$

$\displaystyle {{A}^{15}}=\left( \begin{matrix} 1 & 15(-3) \\ 0 & 1 \\ \end{matrix} \right)=\left( \begin{matrix} 1 & -45 \\ 0 & 1 \\ \end{matrix} \right)$