Son Yazılar :
NKFUCOM
NKFUCOM

Yamuk Çeşitleri ve Özellikleri

4
By on Bilgi Dünyası

Yamuk nedir? Yamuk çeşitleri, yamuk formülleri, özellikleri, alanı. çevresi, açıları ile ilgili kurallar, örnekler.

YAMUK

İki kenarı paralel, diğer iki kenarı paralel olmayan konveks dörtgene yamuk denir.

Paralel olan kenarlara yamuğun tabanları ve paralel olmayan kenarların orta noktalarını birleştiren doğru parçasına da yamuğun orta tabanı adı verilir.

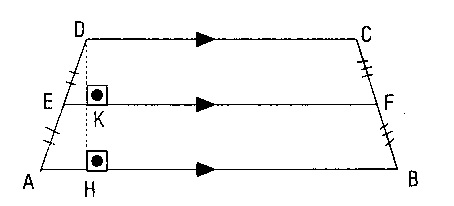
yamuk

\displaystyle \left[ AB \right]\parallel \left[ EF \right]\parallel \left[ CD \right]

\displaystyle \left| DH \right|=h,\left| AB \right|=a;\left| CD \right|=c;\left| EF \right|=e olmak üzere,

A) \displaystyle \left| EF \right|=\frac{a+c}{2}

B) \displaystyle \left| DK \right|=\left| KH \right|=\frac{h}{2}

C) \displaystyle A\left( ABCD \right)=\frac{\left( a+c \right).h}{2}=e.h

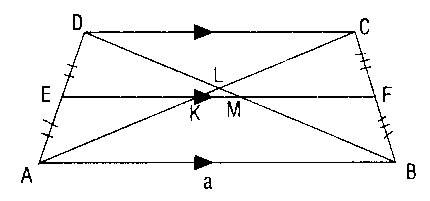
D) yamuk-ozellikleri-1

\displaystyle \left| AK \right|=\left| KC \right|

\displaystyle \left| MB \right|=\left| MD \right|

\displaystyle \left| EK \right|=\left| MF \right|=\frac{c}{2}

\displaystyle \left| KM \right|=\frac{a-c}{2}

E) \displaystyle \left[ MN \right]\parallel \left[ AB \right]

\displaystyle \frac{1}{x}=\frac{1}{a}+\frac{1}{c}

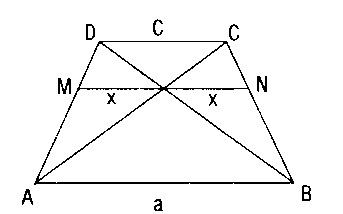
yamuk-ozellikleri-2

F) \displaystyle \left| OE \right|=\frac{c.h}{a+c}

\displaystyle \left| OF \right|=\frac{a.h}{a+c}

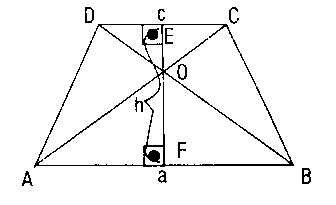
yamuk-ozellikleri-3

G) \displaystyle {{S}_{1}}+{{S}_{4}}={{S}_{2}}+{{S}_{3}}
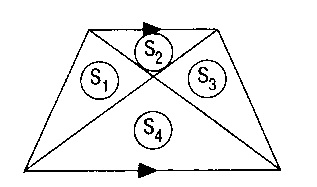
(taban ve yükseklikleri aynı olan üçgenler)

\displaystyle {{S}_{1}}={{S}_{3}}=\sqrt{{{S}_{2}}.{{S}_{4}}}

\displaystyle A\left( ABCD \right)=S={{\left( \sqrt{{{S}_{2}}}+\sqrt{{{S}_{4}}} \right)}^{2}}

yamuk-ozellikleri-4

H) Dik Yamuk

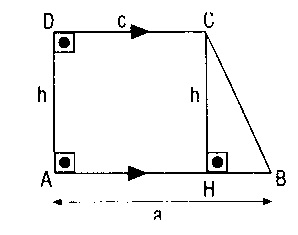
dik-yamuk

Dik yamukta köşegenler dik kesişiyorlarsa,

\displaystyle h=\sqrt{ac} ‘dir.

İ) ikizkenar Yamuk:

Yan kenarları eşit olan yamuktur.

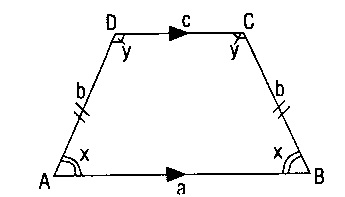
ikizkenar-yamuk

I- Taban açıları eştir.

II- Tavan açıları eştir.

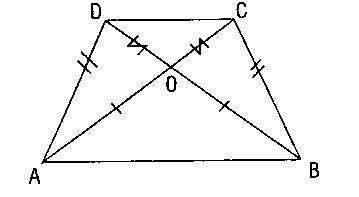
ikizkenar-yamuk-1

III- Köşegenler eşittir

|AC|=|DB|
|AO|=|OB|
|DO|=|OC|

IV- 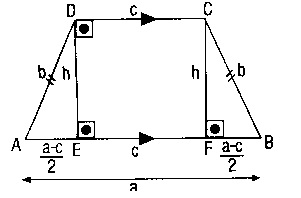yamuk-ozellikleri-5

\displaystyle \left| AE \right|=\left| FB \right|=\frac{a-c}{2}

V- 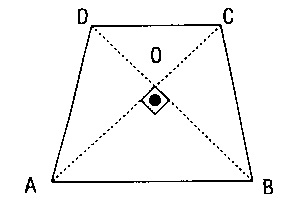yamuk-ozellikleri-6

Köşegenler birbirine dikse; h² = a.c olur.

VI- 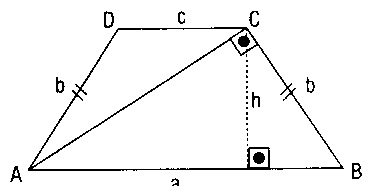yamuk-ozellikleri-7

Köşegenlerin yan kenarları dikse;

\displaystyle h=\frac{\sqrt{{{a}^{2}}-{{c}^{2}}}}{2}


4 yorum

Leave A Reply