Kaos kuramı nedir, neyi savunur? Kaos kuramının ortaya çıkışı, gelişimi nasıl olmuştur? Kelebek etkisi nedir, hakkında bilgi.
Kaos Kuramı
Kaos kuramı, koşullardaki çok küçük değişikliklerin ileride çok büyük sonuçlara yol açabileceğini söyler. Evden 30 saniye geç çıksaydınız, belki otobüsü kaçıracaktınız ama aynı zamanda sizi yeni bir işe yönlendirerek yaşamınızın akışını değiştirecek kişiyle de tanışacaktınız. Kaos kuramının en bilinen uygulama alanı hava durumudur. “Kelebek etkisi” adıyla bilinen olguda, küçük bir rüzgârcık, gezegenin bir başka yerinde kasırgaya yol açabilir. Ancak kaos gerçek anlamda kaotik değildir; içinde birtakım kalıplar barındırır.
Kaos kuramına göre, Brezilya’da bir kelebeğin kanat çırpması Teksas’ta bir hortuma neden olabilir. Bazı sistemlerde başlangıç koşullarının çok benzer olmasına karşın, sonuçlar çok farklı olabilir. Hava durumu bu tür bir sistemdir. Bir yerin sıcaklığında ya da basıncındaki çok küçük bir değişiklik bir başka bölgede şiddetli yağışa yol açacak zincirleme bir dizi olayı tetikleyebilir.
Aslında kaos pek doğru bir adlandırma değildir. Çünkü sözcüğün akla getirdiği gibi tümüyle rassal, öngörülemez ve gelişigüzel yapılı değildir. Kaotik sistemler de aslında deterministiktir, yani başlangıç noktası kesin olarak bilinirse öngörülmeleri ve tekrarlanmaları mümkündür. Basit fizik kurallarıyla pek çok olay açıklanabilir ki bunlar her denemede aynı sonucu verir. Ama bir sonuca bakarak nasıl meydana geldiğini kesin olarak söylemek imkânsızdır, çünkü aynı sonuca birden fazla yoldan ulaşılmış olabilir. Bir sonucu tetikleyen başlangıç koşullarıyla bir başka sonucu tetikleyenler arasındaki farklar çok küçük, hatta ölçülemeyecek kadar küçük olabilir. Yani girdilerdeki çok küçük farklar birbirinden çok farklı sonuçlar doğurabilir.
Bu çeşitlilikten dolayı eğer girdi değerlerinde bir belirsizlik varsa, izleyen geliş’ meler yelpazesi çok geniş olabilir. Hava durumu örneğinde, eğer rüzgârcığın sıcaklığı düşündüğünüzden bir dereceden daha az bile farklı olsa, öngörünüz tamamen yanlış çıkabilir ve komşu kasabada şiddetli bir fırtına yerine kısa süreli bir yağış yada güçlü bir hortum gerçekleşebilir. Bu nedenle hava durumu tahmincileri iklim modelini çıkaracakları zaman dilimini sınırlı tutar. Atmosferin durumuyla ilgili olarak, yeryüzündeki meteoroloji istasyonlarından ve yörüngedeki çok sayıda uydudan muazzam miktarda veri bile gelse, tahminciler en çok birkaç günlük hava durumunu öngörebilirler. Bu sürenin ötesinde belirsizlikler, kaos kuramı gereği çok büyük hale gelmeye başlar.
Gelişimi
Kaos kuramı 1960’lı yıllarda Amerikalı matematikçi ve meteorolog Edward”Lorenz tarafından geliştirildi. Hava durumu modellemesi için bilgisayar kullanan Lorenz, hesapları kolaylaştırmak için simülasyonu parçalara ayırmıştı. Simülasyonu bir sonraki sefer ortasından başlatabilmek için sayıların çıktılarını aldı. Bilgisayarın belleği sayıları virgülden sonra altı hane olarak tutarken, çıktılarda gözüken sayılar virgülden sonraki ilk üç haneye kadar yuvarlanmıştı. Örneğin 0,123456 sayısı çıktıda 0,123 olarak gözüküyordu ve Lorenz bilgisayara sayıları bu yeni halleriyle girdi. Ve hava durumu tahminlerinin ilk seferden tamamen farklı olduğunu gördü. Bilgisayarın sayıları yuvarlanmasından kaynaklanan küçücük farklar, sürecin sonundaki hava durumu tahmin örüntülerini bambaşka hale getiriyordu. Kullandığı modeller yeniden üretilebilir modellerdi, yani rassal değillerdi. Ortaya çıkan farkları yorumlamak zordu. Bu kadar küçük farklar bu kadar büyük oynamalara nasıl yol açabilirdi?
Daha dikkatli inceleyince ortaya çıkan hava durumu tahmin örüntülerinin belli bir kümeyle sınırlı olduğunu gördü ve bunlara “garip çeker” adını verdi. Girdiler değiştirilerek her türlü hava durumu tahmini üretilemiyordu. Her ne kadar girdi olarak verilen sayılara bakarak önceden tahmin etmesi güç olsa da ancak belli bir hava durumu örüntü kümesi ortaya çıkıyordu. Bu kaotik sistemlerin temel özelliğidir. Belli bazı örüntüler izlerler ama belli bir sonuçtan geriye gidilerek belli bir başlangıç noktasına ulaşılamaz. Çünkü aynı sonuca götüren birçok farklı yol vardır.
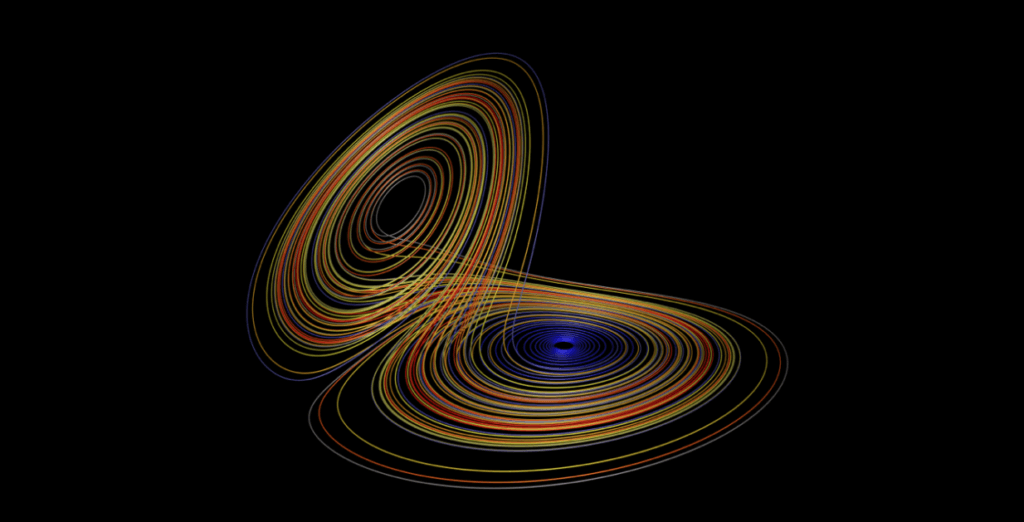
Girdi ile çıktı arasındaki bağlantılar grafiksel olarak izlenebilir. Böylece tek bir kaotik sistemin ne kadar çeşitli davranış şekli olabildiği görülür. Bu tür grafikler garip çekerlerin haritasını verir. En ünlü örneklerinden biri, üst üste gelmiş ve biraz kaydırılıp şekli bozulmuş çok sayıda sekizden oluşan ve bir kelebeğin kanatlarını andıran Lorenz çekim bölgesidir.
Kaos kuramı da fraktalların keşfedildiği dönemde ortaya çıkmıştır. Gerçekte bu ikisi yakından ilişkilidir. Birçok sistemin kaos çözümlerinin çekim bölgesi haritaları fraktallar şeklindedir. Çekim bölgesinin ayrıntılı yapısı, birçok ölçekte kendini yineleyen bir yapıdır.

Kelebek etkisi
Kaosun temel fikri olan “küçük değişikliklerin ileride büyük sonuçlar doğurabileceği” fikri, “kelebek etkisi” adıyla bilinir. Lorenz bununla bir kelebeğin kanat çırpışlarının bir başka yerde kasırgaya yol açabileceğini kastetmiştir. Bu fikir özellikle zaman yolculuğuyla birlikte popüler kültürde ve filmlerde -Jurassic Park ve Kelebek Etkisi filmlerinde olduğu gibi— yaygın olarak kullanılmıştır. 1946’da çevrilen Şahane Hayat (It’s a Wonderful Life) filminin ana karakteri olan George’a bir melek, eğer o doğmamış olsaydı kasabanın ne kadar içler acısı bir durumda olacağını gösterir. Melek şöyle der: “Sana büyük bir armağan verildi George; sensiz bir dünyanın nasıl bir yer olacağını görme şansı.” George kendi varlığının bir adamı boğulmaktan kurtardığını ve yaşamının da aslında şahane olduğunu fark eder.
İlk Örnekler
Matematikçilerin değişik sayı girdileriyle tekrar tekrar hesap yapmasını sağlayan bilgisayarların kullanımının artması, kaos kuramının hızla gelişmesini sağladı. Gerçi kaotik özellikteki basit sistemler çok daha önceden biliniyordu. Örneğin 19. yüzyılın sonunda bilardo toplarının izleyeceği yolların ya da yörüngelerin kaotik olduğu biliniyordu.
Jacques Hadamard, golf topunun golf sahasında ilerleyişi gibi, parçacıkların kıvrımlı yüzeylerdeki hareketleri üzerine çalışmıştı. Buna “Hadamard bilardosu” denir. Bazı yüzeylerde parçacıkların izlediği yollar kararsızlaşıyor ve parçacıklar kenardan düşüyordu. Diğerleri yüzeyde kalıyor ama değişken yollar izliyorlardı. Bir süre sonra Henri Poincaré de kütleçekim etkisi altındaki üç cismin -örneğin iki uydulu Dünya’nın- yörüngeleri için tekrar etmeyen çözümler, yani kararsız yörüngeler buldu. Üç cisim birbirlerinin çevresinde sürekli değişen halkalar üzerinde ama birbirlerinden hiç kopmadan dönüyorlardı. Bu gelişmelerin ardından, matematikçiler ergodik kuram olarak bilinen çok cisimli hareket kuramını geliştirdiler. Kuramı türbülanslı akışkanlar ve radyo devrelerindeki elektriksel salınmalara uyguladılar. Kaos kuramı 1950’li yıllardan bu yana hem yeni kaotik sistemler bulunduğu için hem de hesapları kolaylaştıran dijital bilgisayarlar yaygınlaştığı için hızla gelişti. İlk bilgisayarlardan ENIAC, kaos araştırmalarında ve hava durumu tahmininde kullanıldı.
Kaotik davranış doğada yaygındır. Kaos hava durumunda ve akışkanların akışlarında görüldüğü gibi, gezegenlerin hareketleri gibi çok cisimli sistemlerdeki hareketlerde de görülür. Neptün’ün bir düzineden fazla uydusu vardır. Bu uydular her yıl aynı yörüngelerde dönmek yerine, kaos nedeniyle her yıl farklı yörüngelere kayarlar. Bazı bilim insanları Güneş Sistemimizdeki düzenin de kaos sayesinde oluşmuş olabileceğini düşünüyor. Bugünkü gezegenler ve başkaları milyarlarca yıl önce dev bir bilardo oyununun parçası oldular, farklı yörüngeler denediler, kararsız olanlar ortadan yok oldu ve geriye gezegenlerin bugün gördüğümüz düzeni kaldı.